题目内容
19.某实验小组利用如图甲所示的气垫导轨实验装置来探究合力一定时,物体的加速度与质量之间的关系.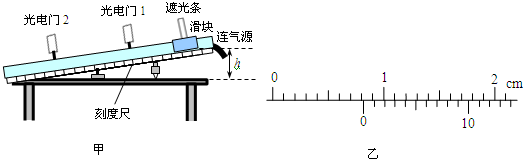
(1)做实验时,将滑块从图甲所示位置由静止释放,由数字计时器(图中未画出)可读出遮光条通过光电门1、2的时间分别为△t1、△t2;用刻度尺测得两个光电门中心之间的距离x,用游标卡尺测得遮光条宽度d.则滑块经过光电门1时的速度表达式v1=$\frac{d}{△{t}_{1}}$;经过光电门2时的速度表达式v2=$\frac{d}{△{t}_{2}}$,滑块加速度的表达式a=$\frac{{(\frac{d}{△{t}_{2}})}^{2}-{(\frac{d}{△{t}_{1}})}^{2}}{2x}$.(以上表达式均用已知字母表示).如图乙所示,若用20分度的游标卡尺测量遮光条的宽度,其读数为8.15mm.
(2)为了保持滑块所受的合力不变,可改变滑块质量M和气垫导轨右端高度h(见图甲).关于“改变滑块质量M和气垫导轨右端的高度h”的正确操作方法是BC
A.M增大时,h增大,以保持二者乘积增大
B.M增大时,h减小,以保持二者乘积不变
C.M减小时,h增大,以保持二者乘积不变
D.M减小时,h减小,以保持二者乘积减小.
分析 (1)知道光电门测量滑块瞬时速度的原理.根据运动学公式求出加速度.了解不同的测量工具的精确度和读数方法;
(2)根据对滑块的受力分析,写出滑块受到的合力的表达式,然后得出结论.
解答 解:(1)滑块经过光电门1时的速度表达式v1=$\frac{d}{△{t}_{1}}$
经过光电门2时的速度表达式v2=$\frac{d}{△{t}_{2}}$
根据匀变速直线运动位移速度公式得:a=$\frac{{{v}_{2}}^{2}-{{v}_{1}}^{2}}{2x}$=$\frac{{(\frac{d}{△{t}_{2}})}^{2}-{(\frac{d}{△{t}_{1}})}^{2}}{2x}$
游标卡尺的读数由主尺和游标尺两部分组成.读数为8.15mm.
(2)滑块的合力F合=Mg$\frac{h}{x}$,为了保持滑块所受的合力不变,所以M和h 不能同时增大或减小.
故选:BC.
故答案为:(1)$\frac{d}{△{t}_{1}}$;$\frac{d}{△{t}_{2}}$;$\frac{{(\frac{d}{△{t}_{2}})}^{2}-{(\frac{d}{△{t}_{1}})}^{2}}{2x}$;8.15mm;(2)BC
点评 考查通过平均速度求瞬时速度的方法,掌握运动学公式求加速度的应用,知道20分度的游标卡尺的精确度.并能够用力学知识找出M和h的关系

练习册系列答案
相关题目
12.下列情况中运动的人或物体,可以看成质点的是( )
| A. | 研究神舟六号飞船绕地球飞行时的周期 | |
| B. | 研究城际轨道列车从广州到肇庆的时间 | |
| C. | 研究火车通过西江大桥的时间 | |
| D. | 研究跳水运动员郭晶晶的跳水姿态 |
10. 水平地面上有一个倾角为θ的斜面,其表面绝缘.另一个带正电的滑块放在斜面上,两物体均处于静止状态,如图所示.当加上水平向右的匀强电场后,滑块与斜面仍相对地面静止,( )
水平地面上有一个倾角为θ的斜面,其表面绝缘.另一个带正电的滑块放在斜面上,两物体均处于静止状态,如图所示.当加上水平向右的匀强电场后,滑块与斜面仍相对地面静止,( )
 水平地面上有一个倾角为θ的斜面,其表面绝缘.另一个带正电的滑块放在斜面上,两物体均处于静止状态,如图所示.当加上水平向右的匀强电场后,滑块与斜面仍相对地面静止,( )
水平地面上有一个倾角为θ的斜面,其表面绝缘.另一个带正电的滑块放在斜面上,两物体均处于静止状态,如图所示.当加上水平向右的匀强电场后,滑块与斜面仍相对地面静止,( )| A. | 滑块对斜面的压力一定变大 | B. | 斜面体对地面的压力一定变大 | ||
| C. | 滑块与斜面间的摩擦力一定变大 | D. | 滑块与斜面间的摩擦力一定变小 |
8.以下说法中正确的有( )
| A. | 物体运动的速度越大,速度的变化量就越大,加速度也越大 | |
| B. | 在加速上升的电梯中,电梯对人的支持力大于人对电梯的压力 | |
| C. | 合外力做的总功为零,则物体的机械能一定守恒 | |
| D. | E=$\frac{F}{q}$是电场强度的定义式,F是放入电场中的电荷所受的电场力,q是放入电场中电荷的电荷量,它适用于任何电场 |
9. 一理想自耦变压器的原线圈A、B 端接有u=220$\sqrt{2}$sin(100πt)V 的电压,副线圈与定值电阻R1、可调电阻R2连接,触头P与线圈始终接触良好,下列判断正确的是( )
一理想自耦变压器的原线圈A、B 端接有u=220$\sqrt{2}$sin(100πt)V 的电压,副线圈与定值电阻R1、可调电阻R2连接,触头P与线圈始终接触良好,下列判断正确的是( )
 一理想自耦变压器的原线圈A、B 端接有u=220$\sqrt{2}$sin(100πt)V 的电压,副线圈与定值电阻R1、可调电阻R2连接,触头P与线圈始终接触良好,下列判断正确的是( )
一理想自耦变压器的原线圈A、B 端接有u=220$\sqrt{2}$sin(100πt)V 的电压,副线圈与定值电阻R1、可调电阻R2连接,触头P与线圈始终接触良好,下列判断正确的是( )| A. | 电阻R1上电流变化的频率为100Hz | |
| B. | 若原、副线圈匝数比为2:1,则副线圈两端电压有效值为110V | |
| C. | 若触头P不动,增大R2,则R2上消耗的功率一定变小 | |
| D. | 若将触头P向下移动,同时减小R2,则R1上的电流一定增大 |
 如图所示,质量为m1=10kg的滑块置于一粗糙的斜面上,斜面的倾角为30°,用一平行于斜面的大小为60N的力F推滑块,滑块沿斜面向上匀速运动,斜面体质量m2=20kg,且始终静止,取g=10m/s2,求:
如图所示,质量为m1=10kg的滑块置于一粗糙的斜面上,斜面的倾角为30°,用一平行于斜面的大小为60N的力F推滑块,滑块沿斜面向上匀速运动,斜面体质量m2=20kg,且始终静止,取g=10m/s2,求: