题目内容
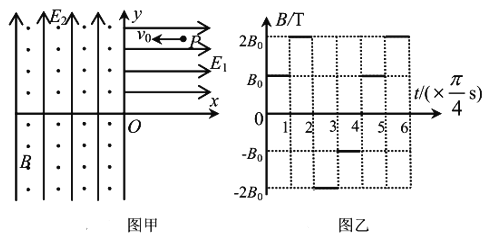
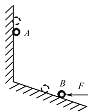
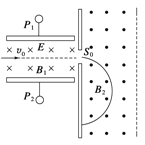
【题目】如图所示,空间存在着方向竖直向上的匀强电场和方向垂直于纸面向内、磁感应强度大小为B的匀强磁场,带电量为+q、质量为r的小球Q静置在光滑绝缘的水平高台边缘,另一质量为m、不带电的绝缘小球P以水平初速度v0向Q运动, ![]() ,小球P、Q正碰过程中没有机械能损失且电荷量不发生转移,已知匀强电场的电场强度
,小球P、Q正碰过程中没有机械能损失且电荷量不发生转移,已知匀强电场的电场强度![]() ,水平台面距地面高度
,水平台面距地面高度![]() ,重力加速度为g,不计空气阻力.
,重力加速度为g,不计空气阻力.
(1)求P、Q两球首次发生弹性碰撞后小球Q的速度大小,
(2)P、Q两球首次发生弹性碰撞后,经过多少时间小球P落体?落地点与平台边缘间的水平距离多大?
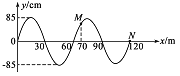
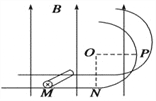
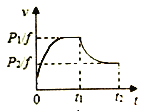
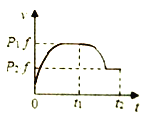
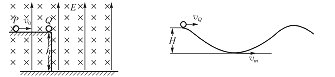
(3)若撤去匀强电场,并将小球Q重新放在平台边缘、小球P仍以水平初速度![]() 向Q运动,小球Q的运动轨迹如图所示,已知Q球在最高点和最低点所受合力的大小相等.求小球Q在运动过程中的最大速度和第一次下降的最大距离H.
向Q运动,小球Q的运动轨迹如图所示,已知Q球在最高点和最低点所受合力的大小相等.求小球Q在运动过程中的最大速度和第一次下降的最大距离H.
【答案】(1) ![]() ,
,![]() (2)
(2) ![]() ,
,![]() (3)
(3) ![]() ,
, ![]()
【解析】(1)小球P、Q首次发生弹性碰撞时,取向右为正方向,由动量守恒和机械能守恒得:
mv0=mvP+mvQ;
![]()
联立解得 vP=0,vQ=v0=![]() .
.
(2)对于小球Q,由于qE=mg,故Q球做匀速圆周运动,由洛伦兹力提供向心力,则
qvQB=m![]()
经时间t1=T=![]()
小球P、Q再次发生弹性碰撞,由(1)可知碰后:vP′=v0=![]() ,vQ′=0
,vQ′=0
小球P离开平台后做平抛运动,平抛运动的时间为t2,t2=![]()
所以P与Q首次发生碰撞后到落地,经过的时间![]()
落地点与平台边缘的水平距离 xP=vP′t2=![]()
(3)PQ相碰后,Q球速度vQ=v0,Q球在最高点和最低点的合力大小相等,故有:
![]()
解得![]()
因为![]()
解得![]()

练习册系列答案
相关题目