题目内容
(8分)土星上空有许多大小不等的岩石颗粒,其绕土星的运动可视为圆周运动。其中有两个岩石颗粒A和B与土星中心距离分别为rA=8.0×104 km和r B=1.2×105 km。忽略所有岩石颗粒间的相互作用。(结果可用根式表示)
⑴求岩石颗粒A和B的线速度之比;
⑵求岩石颗粒A和B的周期之比;
⑶土星探测器上有一物体,在地球上重为10 N,推算出他在距土星中心3.2×105 km处受到土星的引力为0.38 N。已知地球半径为6.4×103 km,请估算土星质量是地球质量的多少倍?
⑴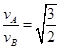 ⑵
⑵ ⑶M0/M=95
⑶M0/M=95
解析试题分析:⑴设土星质量为M0,颗粒质量为m,颗粒距土星中心距离为r,线速度为v,根据牛顿第二定律和万有引力定律: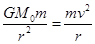 (1分)
(1分)
解得: (1分)
(1分)
对于A、B两颗粒分别有: 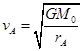 和
和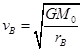
得: 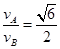 或
或 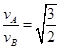 (1分)
(1分)
⑵设颗粒绕土星作圆周运动的周期为T,则: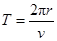 (1分)
(1分)
对于A、B两颗粒分别有: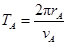 和
和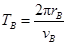
得:  或
或 (1分)
(1分)
⑶设地球质量为M,地球半径为r0,地球上物体的重力可视为万有引力,探测器上物体质量为m0,在地球表面重力为G0,距土星中心r0/=3.2×105 km处的引力为G0/,根据万有引力定律: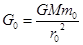 (1分)
(1分)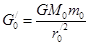 (1分)
(1分)
解得: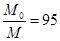 (1分)
(1分)
考点:本题考查对万有引力定律的应用。

练习册系列答案
相关题目
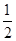 。若不计其他星球的影响,该星球的第一宇宙速度是地球的第一宇宙速度的________倍,某物体在该星球表面上所受重力是在地球表面上所受重力的__________倍。
。若不计其他星球的影响,该星球的第一宇宙速度是地球的第一宇宙速度的________倍,某物体在该星球表面上所受重力是在地球表面上所受重力的__________倍。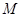 ,半径为
,半径为 ,万有引力常量为
,万有引力常量为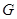 .请你结合以上数据求:
.请你结合以上数据求: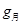 ; ②月球的第一宇宙速度
; ②月球的第一宇宙速度 ;
; 倍)利用太阳能发电,然后通过微波持续不断地将电力输送到地面,这样就建成了太阳能发电站。求卫星在地球同步轨道上向心加速度的大小(答案保留两位有效数字);
倍)利用太阳能发电,然后通过微波持续不断地将电力输送到地面,这样就建成了太阳能发电站。求卫星在地球同步轨道上向心加速度的大小(答案保留两位有效数字);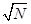 (N>1),为了解释T观测与T计算的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质,作为一种简化模型,我们假定在这两个星体边线为直径的球体内均匀分布着暗物质,而不考虑其它暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
(N>1),为了解释T观测与T计算的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质,作为一种简化模型,我们假定在这两个星体边线为直径的球体内均匀分布着暗物质,而不考虑其它暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
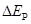 ;②从碰后至返回到碰撞点的过程中,弹簧对物体B冲量的大小。
;②从碰后至返回到碰撞点的过程中,弹簧对物体B冲量的大小。