题目内容
放在水平地面上的物体受到水平拉力的作用，在0～6 s内其速度与时间图象和拉力的功率与时间图象分别如图（甲）、（乙）所示，则物体的质量为（取g="10" m／s2）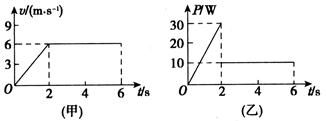
A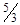． ㎏ | B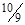． ㎏ | C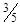． ㎏ | D． ㎏ |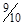
B
解析试题分析：在0-2s物体做匀加速直线运动，其加速度为a=Δv/Δt=3m/s2,2s时其拉力的功率为P=30W=Fv,此时速度v=6m/s，则拉力F=P/v=5N，有F-f=ma；2-6s时物体做匀速直线运动，此时有功率不变，则有P’=FV=fv,则f=5/3N，将此代入F-f=ma有，5-5/3=3m得到m=10/9kg。所以B选项正确。
考点：本题考查对机车启动过程是理解和对牛顿第二定律的应用。
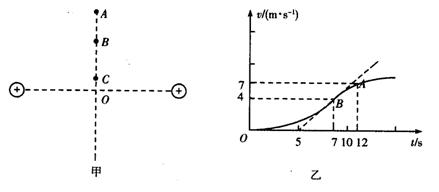
下列有关运动的说法正确的是：（ ）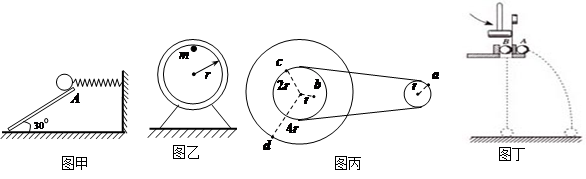
| A．图甲中撤掉挡板A的瞬间，小球的加速度竖直向下 |
| B．图乙中固定在竖直面内的圆环内径r=1.6m，小球沿内圆表面过最高点速度可以为2m/s |
| C．图丙中皮带轮上b点的加速度小于a点的加速度 |
| D．图丁中用铁锤水平打击弹簧片后，B球比A球先着地 |
如图5所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力．已知AP＝2R，重力加速度为g，则小球从P到B的运动过程中 
| A．重力做功2mgR | B．机械能减少mgR | C．合外力做功mgR | D．克服摩擦力做功 mgR |
如图所示，小物块从光滑的倾斜轨道上的Ｐ点自由滑下，到达底端后滑上一水平传送带（轨道底端与传送带表面相齐平）。当传送带静止时，小物块通过传送带后水平飞出落到地面上，物块与皮带因摩擦产生的热量为Q。当皮带轮按逆时针方向匀速转动时，则小物块从Ｐ点自由滑下后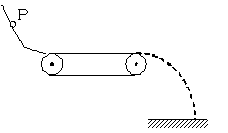
| A．有可能滑不到传送带右端 |
| B．能通过传送带，但落点会变得近一些 |
| C．能通过传送带，但摩擦产生的热量大于Q |
| D．能通过传送带，但物体克服摩擦力做的功大于Q |
长为L的轻杆一端固定质量为m的小球，另一端可绕固定光滑水平转轴O转动。现使小球在竖直平面内做圆周运动，C为圆周的最高点，若小球通过圆周最低点D的速度大小为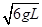
，不计一切阻力，则小球过C点时
| A．速度大小等于0 |
B．速度大小等于 |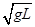
| C．受到轻杆向上的弹力，大小为mg |
| D．受到轻杆向下的弹力，大小为mg |
如图，水平传送带保持 1 m/s 的速度运动．一质量为1 kg的物体与传送带间的动摩擦因数为0.2，现将该物体无初速地放到传送带上，则物体在运动1m的过程中，皮带对该物体做的功为（g ="10" m/s2）（ ）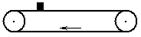 
| A．0.5J | B．2J | C．2.5J | D．5J |
如图所示，细线的一端系一质量为m的小球，另一端固定在倾角为θ的光滑斜面体顶端，细线与斜面平行．在斜面体以加速度a水平向右做匀加速直线运动的过程中，小球始终静止在斜面上，重力加速度为g，小球受到细线的拉力为T，斜面的支持力为FN，则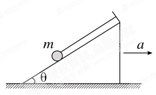
| A．T＝m(g sinθ＋a cosθ) |
| B．T＝m(g cosθ＋a sinθ) |
| C．FN＝m(g cosθ－a sinθ) |
| D．FN＝m(g cosθ＋a sinθ) |