题目内容
长为L的轻杆一端固定质量为m的小球，另一端可绕固定光滑水平转轴O转动。现使小球在竖直平面内做圆周运动，C为圆周的最高点，若小球通过圆周最低点D的速度大小为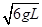
，不计一切阻力，则小球过C点时
| A．速度大小等于0 |
B．速度大小等于 |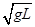
| C．受到轻杆向上的弹力，大小为mg |
| D．受到轻杆向下的弹力，大小为mg |
D
解析试题分析：根据机械能守恒定律，则小球从D点到C点可得 
，解得
;此时对小球根据牛顿定律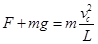 
,解得 F=mg，方向向下。选项D正确。
考点：机械能守恒定律及牛顿定律。
如图所示，水平放置的传送带以v =" 2" m/s的速度向右运行，现将一质量为m =" 1" kg的小物体轻轻地放在传送带的左端，物体与传送带间的动摩擦因数μ＝0.2，左端与右端相距4m，则小物体从左端运动到右端所需时间及此过程中由于摩擦产生的热量分别为（g10m/s2）
| A．2s 2J | B．2s 8J | C．2.5s 2J | D．2.5s 8J |
如图，质量分别为mA和mB的两小球带有同种电荷，电荷量分别为qA和qB，用绝缘细线悬挂在天花板上。平衡时，两小球恰处于同一水平位置，细线与竖直方向间夹角分别为q1与q2（q1＞q2）。两小球突然失去各自所带电荷后开始摆动，最大速度分别为vA和vB，最大动能分别为EkA和EkB。则不正确的是
| A．mA一定小于mB | B．qA一定大于qB | C．vA一定大于vB | D．EkA一定大于EkB |
㎏
㎏
㎏
㎏如图所示，穿在水平直杆上质量为m的小球开始时静止.现对小球沿杆方向施加恒力F0，垂直于杆方向施加竖直向上的力F，且F的大小始终与小球的速度成正比，即F=kυ(图中未标出)。已知小球与杆间的动摩擦因数为μ，已知小球运动过程中未从杆上脱落，且F0>μmg.下列说法正确的是：
| A．小球先做加速度减小的加速运动,后做加速度增大的减速运动直到静止 |
| B．小球先做加速度增大的加速运动,后做加速度减小的加速运动，直到最后做匀速运动 |
C．小球的最大加速度为 |
D．恒力F0,的最大功率为 |
两端开口的U形细管内装有一定量的水置于竖直面内，开口竖直向上，静止时两竖管内水面相平，由于细管的某种运动，管内水面形成如图所示的高度差，在下列描述的各种运动中，细管可能的运动是( )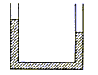
| A．水平向右加速运动 |
| B．水平向左匀速运动 |
| C．绕某一竖直轴旋转运动 |
| D．自由落体运动 |
如图所示为杂技“顶杆”表演，一人站在地上，肩上扛一质量为M的竖直竹竿，当竿上一质量为m的人以加速度a加速下滑时，杆对地面上的人的压力大小为( )
| A．（M+m）g－ma | B．（M+m）g+ma |
| C．（M+m）g | D．（M－m）g |
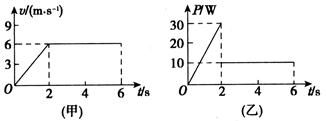
一滑块在水平地面上沿直线滑行，t=0时其速度为2.0m/s。从此刻开始在滑块运动方向上再施加一水平拉力F，力F和滑块的速度v随时间t的变化规律分别如图甲和乙所示。设在第1s内、第2s内、第3s内力F对滑块做功的平均功率分别为P1、P2、P3，则 （ ）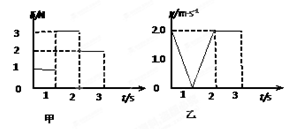
| A．P1>P2>P3 |
| B．P1<P2<P3 |
| C．0~2s内力F对滑块做功为4J |
| D．0~2s内摩擦力对滑块做功为4J |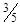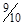