题目内容
8.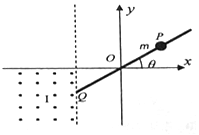 如图所示,竖直平面内的直角坐标系xoy中,在x<0的区域内存在竖直方向的匀强电场(图中未画出),第三象限内平行于y轴的虚线左侧区域Ⅰ中还存在方向垂直于纸面向外的匀强磁场,有一长为8.5L的绝缘粗糙直杆沿与x轴正方向成θ=37°固定放置,其PQ段中点恰好与坐标原点O重合,端点Q在区域Ⅰ的边界上,质量为m、电荷量为q(q>0)的小球(可视为质点)穿在直杆上,小球可在杆上只有滑动,将小球从P点静止释放,小球沿杆运动,随后从Q端离开直杆进入区域Ⅰ,小球在区域Ⅰ中恰好做匀速圆周运动,一段时间后垂直穿过x轴,已知PQ段长度为L,小球和杆之间的动摩擦因数μ=0.5,整个过程中小球所带电荷量不变,重力加速度为g,sin37°=0.6,cos37°=0.8,求
如图所示,竖直平面内的直角坐标系xoy中,在x<0的区域内存在竖直方向的匀强电场(图中未画出),第三象限内平行于y轴的虚线左侧区域Ⅰ中还存在方向垂直于纸面向外的匀强磁场,有一长为8.5L的绝缘粗糙直杆沿与x轴正方向成θ=37°固定放置,其PQ段中点恰好与坐标原点O重合,端点Q在区域Ⅰ的边界上,质量为m、电荷量为q(q>0)的小球(可视为质点)穿在直杆上,小球可在杆上只有滑动,将小球从P点静止释放,小球沿杆运动,随后从Q端离开直杆进入区域Ⅰ,小球在区域Ⅰ中恰好做匀速圆周运动,一段时间后垂直穿过x轴,已知PQ段长度为L,小球和杆之间的动摩擦因数μ=0.5,整个过程中小球所带电荷量不变,重力加速度为g,sin37°=0.6,cos37°=0.8,求(1)场强的大小及方向
(2)磁感应强度的大小
(3)若改变小球在直杆上静止释放的位置,求小球从Q点经磁场偏转后直接到达x轴的时间.
分析 (1)由于小球在Ⅰ区受三个力作用做匀速圆周运动,则其中的重力及电场力平衡,从而求出电场强度的大小和方向.
(2)从P点到Q点由动能定理求出进入磁场的速度,由于是垂直到达x轴,所以很容易确定小球做匀速圆周运动的圆心和半径,由洛仑兹力提供向心力求出磁感应强度.
(3)同样道理,从横坐标x处自由滑下的小球由动能定理求出进入磁场的速度,由于半径发生变化,画出轨迹,由几何关系求出小球转过的角度,由周期公式从而求出从Q点到达x轴的时间.
解答  解:(1)由题意,小球进入Ⅰ区后恰好做匀速圆周运动,则可知:Eq=mg
解:(1)由题意,小球进入Ⅰ区后恰好做匀速圆周运动,则可知:Eq=mg
所以x<0区的电场强度E=$\frac{mg}{q}$ 方向竖直向上.
(2)从P到Q点,由动能定理得:$mglsinθ-μmgcosθ•\frac{l}{2}-Eq\frac{l}{2}sinθ=\frac{1}{2}m{v}^{2}$
代入可得:v=$\frac{\sqrt{5gl}}{5}$=$\sqrt{2l}$
由于粒子做匀速圆周运动垂直打在x轴上,由几何关系就能求出做匀速圆周运动的半径为:r=$\frac{l}{2}$tgθ=$\frac{3}{8}l$
由洛仑兹力提供向心力,有:$qvB=m\frac{{v}^{2}}{r}$
就能求得:B=$\frac{8\sqrt{2}m}{3q\sqrt{l}}$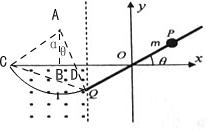
(3)设小球从横坐标为x处自由滑下,由动能定理可得:$mg(xtgθ+\frac{l}{2}sinθ)-μmgcosθ•\frac{x}{cosθ}-Eq\frac{l}{2}sinθ$=$\frac{1}{2}mv{′}^{2}$
从而求$v′=5\sqrt{x}$
在Ⅰ区内做匀速圆周运动,由上述结论半径为:r=$\frac{mv′}{qB}$=$\frac{15}{8}\sqrt{lx}$
由几何关系有:cosα=$\frac{AB}{r}=\frac{(r-\frac{l}{2}tgθ)}{cosθ•r}$=$\frac{5}{4}-\frac{15l}{32r}$=$\frac{5}{4}-\frac{3l}{32\sqrt{x}}$
小球离开杆到达x轴的时间为:t=$\frac{α+θ}{2π}T$=$\frac{arccos(\frac{5}{4}-\frac{3l}{32\sqrt{x}})+θ}{960}π\sqrt{2l}$ (其中α、θ均有°表示)
答:(1)场强的大小是$\frac{mg}{q}$,方向为竖直向上.
(2)磁感应强度的大小为$\frac{8\sqrt{2}m}{3q\sqrt{l}}$.
3)若改变小球在直杆上静止释放的位置,小球从Q点经磁场偏转后直接到达x轴的时间为$\frac{arccos(\frac{5}{4}-\frac{3l}{32\sqrt{x}})+θ}{960}π\sqrt{2l}$.
点评 本题要注意的几个问题:①是由于重力与电场力抵消,所以小球从O点到Q点也不受支持力和摩擦力,合力为零,做匀速直线运动.②第三问先假设从横坐标x处自由滑下,求出进入磁场的速度,确定圆心和半径,求出转过的角度,从而也就求出了时间.

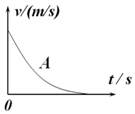 在t=0时,A、B两物体在同一地点以相同的初速度沿同一方向运动,A物体的v-t图象如图,B物体做匀减速直线运动,直到停止,两物体的位移相同,下列说法正确的是( )
在t=0时,A、B两物体在同一地点以相同的初速度沿同一方向运动,A物体的v-t图象如图,B物体做匀减速直线运动,直到停止,两物体的位移相同,下列说法正确的是( )| A. | B运动的时间可能等于A | |
| B. | 在途中B始终在A的前方 | |
| C. | 在途中任一时刻两物体的速度不可能相同 | |
| D. | 在途中任一时刻两物体的加速度不可能相同 |
 如图所示,放在水平面上的物体A用轻绳通过光滑定滑轮连接另一物体B,并静止,这时A受到水平面的支持力为FN,摩擦力为Ff,若把A向左移动一些后,A仍静止,则( )
如图所示,放在水平面上的物体A用轻绳通过光滑定滑轮连接另一物体B,并静止,这时A受到水平面的支持力为FN,摩擦力为Ff,若把A向左移动一些后,A仍静止,则( )| A. | FN将增大 | B. | Ff将减小 | ||
| C. | 轻绳拉力将减小 | D. | 物体A所受合力将增大 |
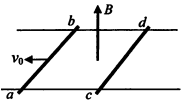 如图所示,一水平面内固定两根足够长的光滑平行金属导轨,导轨上面横放着两根完全相同的铜棒ab和cd,构成矩形回路,在整个导轨平面内都有竖直向上的匀强磁场B.开始时,棒cd静止,棒ab有一个向左的初速度v0,则关于两棒以后的运动,下列说法正确的是( )
如图所示,一水平面内固定两根足够长的光滑平行金属导轨,导轨上面横放着两根完全相同的铜棒ab和cd,构成矩形回路,在整个导轨平面内都有竖直向上的匀强磁场B.开始时,棒cd静止,棒ab有一个向左的初速度v0,则关于两棒以后的运动,下列说法正确的是( )| A. | ab棒做匀减速直线运动,cd棒做勻加速直线运动 | |
| B. | ab棒减小的动量等于cd棒增加的动量 | |
| C. | ab棒减小的动能等于cd棒增加的动能 | |
| D. | 两棒一直运动,机械能不断转化为电能 |
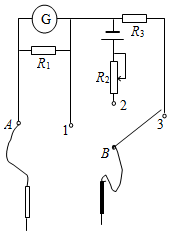 如图所示为一个多用电表的简化电路图,其中表头G的电阻Rg=30?,满偏电流Ig=1mA,R1=0.05?,R2=10k?是滑动变阻器,R3=2970?是定值电阻,电源电动势E=3V,内阻忽略不计,下列说法正确的是( )
如图所示为一个多用电表的简化电路图,其中表头G的电阻Rg=30?,满偏电流Ig=1mA,R1=0.05?,R2=10k?是滑动变阻器,R3=2970?是定值电阻,电源电动势E=3V,内阻忽略不计,下列说法正确的是( )| A. | 当选择开关接1时,测量的是电压 | |
| B. | 当选择开关接2时,测量的是电阻 | |
| C. | 当选择开关接3时,测量的是电流 | |
| D. | 测量时,电流是由A表笔流出,B表笔流入 |
| A. | 伽利略的斜面理想实验是采用了“猜想-假设-证明”的物理归纳法得出结论的 | |
| B. | 卡迪文许是世界物理学史上第一个利用扭秤实验精确测量出了静电力k的常量 | |
| C. | 研究共点力合成的实验从力的等效性出发,利用到了等效替代的物理思想方法 | |
| D. | 重力加速度g是由地球对地球表面上的物体吸引而产生的,g的大小是定值10 |
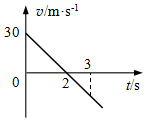 质量为4kg的质点在外力作用下沿直线运动的v-t图象如图所示.则前3s内外力功率的最大值为1800W,3s内外力的平均功率为450W.
质量为4kg的质点在外力作用下沿直线运动的v-t图象如图所示.则前3s内外力功率的最大值为1800W,3s内外力的平均功率为450W.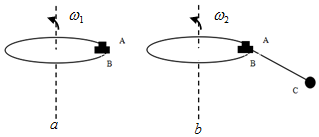
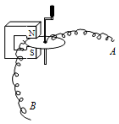 如图所示是世界上早期制作的发电机及电动机的实验装置,有一个可绕固定转轴转动的铜盘,铜盘的一部分处在蹄形磁铁当中.实验时用导线A连接铜盘的中心,用导线B连接铜盘的边缘.若用外力摇手柄使得铜盘顺时针转动起来时,电路闭合会产生感应电流,则电流从B端流出;若将A、B导线端连接外电源,则铜盘会逆时针转动起来,则此时A端连接电源的正极(均选填A或B).
如图所示是世界上早期制作的发电机及电动机的实验装置,有一个可绕固定转轴转动的铜盘,铜盘的一部分处在蹄形磁铁当中.实验时用导线A连接铜盘的中心,用导线B连接铜盘的边缘.若用外力摇手柄使得铜盘顺时针转动起来时,电路闭合会产生感应电流,则电流从B端流出;若将A、B导线端连接外电源,则铜盘会逆时针转动起来,则此时A端连接电源的正极(均选填A或B).