题目内容
【题目】为了使航天员能适应在失重环境下的工作和生活，国家航天局组织对航天员进行失重训练时需要创造出一种失重环境．如图所示，航天员乘坐在总质量
m=5×104 kg的训练飞机上，飞机以200m/s的速度沿30°倾角匀速爬升到
7000m高空时向上拉起，沿竖直方向以v0=200m/s的初速度向上做匀减速直线运动，匀减速的加速度大小为g．当飞机到最高点后立即掉头向下，沿竖直方向以加速度g做加速运动，在这段时间内创造出完全失重的环境．
当飞机离地2 000m高时，为了安全必须拉起，之后又可一次次重复为航天员提供失重训练．若飞机飞行时所受的空气阻力Ff=kv（k=900Ns/m），每次飞机速度达到350m/s后必须终止失重训练（否则飞机可能失控）．（整个运动空间重力加速度g的大小均为10m/s2），求：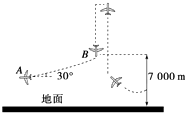
（1）飞机一次上下运动为航天员创造的完全失重的时间；
（2）飞机从最高点下降到离地4 500m时飞机发动机的推力．
【答案】
（1）
解：上升时间为：t上= 
= 
=20 s
上升高度为：h上= 
= 
=2 000 m
竖直下落当速度达到v1=350 m/s时，下落高度
h下= 
= 
=6 125 m
此时飞机离地高度为：△h=h+h上﹣h下=7 000 m+2 000 m﹣6 125 m=2 875 m＞2 000 m
所以 t下= 
= 
=35 s
飞机一次上下为航天员创造的完全失重的时间为：t=t上+t下=20 s+35 s=55 s
（2）
解：飞机离地4 500 m＞2 875 m时，仍处于完全失重状态，飞机自由下落的高度为：
h2=2 000 m+7 000 m﹣4 500 m=4 500 m
此时飞机的速度为：v2= 
= 
m/s=300 m/s
由于飞机加速度为g，所以推力F推应与空气阻力大小相等，即：
F推=Ff=kv2=900×300 N=2.7×105 N
【解析】（1）飞机先以加速度g减速上升，再以加速度g加速下降，达到350m/s时，结束训练周期，根据运动学公式列式计算即可；（2）飞机下降离地4 500m时，飞机处于完全失重状态，根据牛顿第二定律列式求解．
【考点精析】本题主要考查了匀变速直线运动的速度、位移、时间的关系的相关知识点，需要掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值才能正确解答此题．
