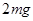题目内容
如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,且2AB=BC。小物块P(可视为质点)与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2。已知P由静止开始从A点释放,恰好能滑动到C点而停下,那么θ、μ1、μ2间应满足的关系是
A.tanθ= B.tanθ=
B.tanθ=
C.tanθ=2μ1-μ2 D.tanθ=2μ2-μ1
A
解析试题分析:A点释放,恰好能滑动到C点,物块受重力、支持力、滑动摩擦力。设斜面AC长为L,对AC过程应用动能定理mgLsinθ-μ1mgcosθ?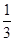 L-μ2mgcosθ?
L-μ2mgcosθ?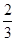 L=0-0=0
L=0-0=0
解得:tanθ= ,A正确。
,A正确。
考点: 本题考查动能定理。

如图, 实线为高速运动正粒子在位于O点的点电荷附近的运动轨迹,M、N和Q为轨迹上的三点,N点离点电荷最近,Q点比M点离点电荷更远,不计正粒子的重力,则( )
| A.正粒子在M点的速率比在Q点的大 |
| B.三点中,正粒子在N点的电势能最小 |
| C.在点电荷产生的电场中,M点的电势比Q点的低 |
| D.正粒子从M点运动到Q点,电场力对它做的总功为正功 |
如图所示,表面粗糙的斜面固定于地面上,并处于方向垂直于纸面向外、磁感应强度为B的匀强磁场中.质量为m、带电荷量为+Q的小滑块从斜面顶端由静止下滑.在滑块下滑的过程中,下列判断正确的是( )
| A.滑块受到的摩擦力不变 |
| B.滑块到达地面时的动能与B的大小无关 |
| C.滑块受到的洛伦兹力方向垂直斜面向下 |
| D.B很大时,滑块可能静止于斜面上 |
如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为 . 若小物体电荷量保持不变,OM=ON,则( )
. 若小物体电荷量保持不变,OM=ON,则( )
A.小物体上升的最大高度为 |
| B.从N到M的过程中,小物体的电势能逐渐减小 |
| C.从M到N的过程中,电场力对小物体先做负功后做正功 |
| D.从N到M的过程中,小物体受到的摩擦力和电场力均是先增大后减小 |
如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g。物块上升的最大高度为H,则此过程中,物块的( )
| A.动能损失了2mgH | B.动能损失了mgH |
| C.机械能损失了mgH | D.机械能损失了 |
如图所示,实线为电场线,虚线为等势线,且相邻两条等势线间的电势差相等。一正电荷(只在电场力的作用下)在φ3上时,具有的动能是20eV,它运动到等势线φ1上时,速度为零。令φ2=0。那么该电荷的电势能为4 eV时,其动能大小为: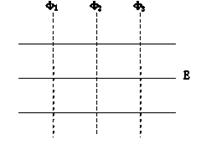
| A.16eV | B.6eV | C.10eV | D.4eV |
在光滑的水平面内有一沿x轴的静电场,其电势 随x坐标值的变化图线如图所示。一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动。下列叙述正确的是( )
随x坐标值的变化图线如图所示。一质量为m,带电量为q的带正电小球(可视为质点)从O点以初速度v0沿x轴正向移动。下列叙述正确的是( )
| A.若小球能运动到x1处,则该过程小球所受电场力逐渐增大 |
| B.带电小球从x1运动到x3的过程中,电势能先减小后增大 |
C.若该小球能运动到x4处,则初速度v0至少为 |
D.若v0为 ,带电粒子在运动过程中的最大速度为 ,带电粒子在运动过程中的最大速度为 |
如图所示,一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度大小为3g/4,这个物体在斜面上升的最大高度为h,则这个过程中,下列判断正确的是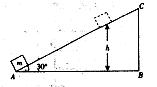
A.重力势能增加了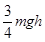 |
B.动能减少了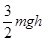 |
C.机械能减少了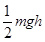 |
| D.物体克服摩擦力的功率随时间在均匀减小 |
 ,用丝线悬挂于O点,在竖直面内摆动,最大摆角为600,水平磁场垂直于小球摆动的平面,当小球自左方摆到最低点时,悬线上的张力恰为零,则小球自右方摆到最低点时悬线上的张力为 ( )
,用丝线悬挂于O点,在竖直面内摆动,最大摆角为600,水平磁场垂直于小球摆动的平面,当小球自左方摆到最低点时,悬线上的张力恰为零,则小球自右方摆到最低点时悬线上的张力为 ( )