题目内容
8. 如图,圆形水平转台半径R=0.5m,上表面离水平地面的高度H=1.25m,小物块A位于转台边缘,与转台中心O距离r=0.3m的小物块B用水平细线与过O点的竖直转轴相连,A、B能随转台一起绕转轴转动,当转台的角速度ω=4rad/s时,物块A刚好要滑离转台、细线断裂,此时转台立即停止转动,设物块所受的最大静摩擦力等于滑动摩擦力,小物块B与转台的动摩擦因素μB=0.1,取g=10m/s2,求:
如图,圆形水平转台半径R=0.5m,上表面离水平地面的高度H=1.25m,小物块A位于转台边缘,与转台中心O距离r=0.3m的小物块B用水平细线与过O点的竖直转轴相连,A、B能随转台一起绕转轴转动,当转台的角速度ω=4rad/s时,物块A刚好要滑离转台、细线断裂,此时转台立即停止转动,设物块所受的最大静摩擦力等于滑动摩擦力,小物块B与转台的动摩擦因素μB=0.1,取g=10m/s2,求:(1)小物块A与转台间的动摩擦因数μA;
(2)小物块B落地点离转台中心O的水平距离L.
分析 (1)根据A恰好滑动,结合最大静摩擦力提供向心力,根据牛顿第二定律求出小物块A与转台间的动摩擦因数μA.
(2)根据线速度与角速度的关系求出B的线速度,结合图中的几何关系求出B离开平台时的位置;然后求出平抛运动的时间,结合初速度求出水平位移,最后再通过几何关系求出物块落地点到转台中心的水平距离.
解答 解:(1)物块A离开转台时,最大静摩擦力提供向心力,
有:${μ}_{A}{m}_{A}g={m}_{A}{ω}^{2}•R$
解得:μA=0.8
(2)平台停止时B的速度:v0=ωr=4×0.3=1.2m/s
B在平台上运动的加速度:$a=\frac{{μ}_{B}{m}_{B}g}{{m}_{B}}={μ}_{B}g=0.1×10=1m/{s}^{2}$
B到平台的边缘的位置如图,由图可知,B到平台的边缘的距离为:
$x=\sqrt{{R}^{2}-{r}^{2}}=\sqrt{{0.5}^{2}-{0.3}^{2}}=0.4$m
B到达平台的边缘时的速度v1,则:
${v}_{1}^{2}-{v}_{0}^{2}=-2ax$
代入数据得:v1=0.8m/s
物块离开平台后做平抛运动,在竖直方向上有:
H=$\frac{1}{2}$gt2
解得t=$\sqrt{\frac{2H}{g}}=\sqrt{\frac{2×1.25}{10}}=0.5$s
在水平方向上有x′=v1t=0.8×0.5=0.4m
物块落地点到转台中心的水平距离L,由L2=(x+x′)2+r2
解得L=$\sqrt{0.73}$m
答:(1)小物块A与转台间的动摩擦因数是0.8;
(2)物块B落地点离转台中心O的水平距离是$\sqrt{0.73}$m.
点评 本题考查了圆周运动和平抛运动的综合,知道圆周运动向心力的来源和平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

 智慧小复习系列答案
智慧小复习系列答案| A. | 时间间隔 | B. | 位移 | C. | 路程 | D. | 速度 |
 如图所示,水平传送带A、B两端相距x=3.5m,物块与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB.下列说法中正确的是( )
如图所示,水平传送带A、B两端相距x=3.5m,物块与传送带间的动摩擦因数μ=0.1,物体滑上传送带A端的瞬时速度vA=4m/s,到达B端的瞬时速度设为vB.下列说法中正确的是( )| A. | 若传送带不动,vB=3 m/s | |
| B. | 若传送带逆时针匀速转动,vB一定等于3 m/s | |
| C. | 若传送带顺时针匀速转动,vB一定大于3 m/s | |
| D. | 若传送带顺时针匀速转动,vB有可能等于3 m/s |
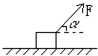 如图所示,位于水平地面上质量为m的木块,在大小为F方向与水平方向成α角的拉力的作用下沿地面作匀加速运动,若木块与地面间动摩擦因数为μ,则木块的加速度大小为( )
如图所示,位于水平地面上质量为m的木块,在大小为F方向与水平方向成α角的拉力的作用下沿地面作匀加速运动,若木块与地面间动摩擦因数为μ,则木块的加速度大小为( )| A. | $\frac{F}{m}$ | B. | $\frac{Fcosα}{m}$ | ||
| C. | $\frac{(Fcosα-μmg)}{m}$ | D. | $\frac{[Fcosα-μ(mg-Fsinα)]}{m}$ |
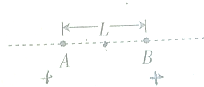 如图所示,真空中有两个带正电的点电荷A、B,它们固定在相距L=0.4m的两点,它们的电荷量分别为Q1=3.6×10-11C,Q2=4.0×10-12C(本题中仅考虑电荷间的库伦力)
如图所示,真空中有两个带正电的点电荷A、B,它们固定在相距L=0.4m的两点,它们的电荷量分别为Q1=3.6×10-11C,Q2=4.0×10-12C(本题中仅考虑电荷间的库伦力) 如图所示,a为一电荷量为q=1.0×10-5C的正点电荷,b为一原来不带电的导体,c、d为导体b内的两点,这两点到点电荷a的距离都等于10cm,当导体b处于静电平衡状态时,导体上的感应电荷在c点和d点产生的电场强度大小分别为Ec=9×106N/C,Ed=9×106N/C.请在图中画出感应电荷在c、d两点产生的电场强度的方向.
如图所示,a为一电荷量为q=1.0×10-5C的正点电荷,b为一原来不带电的导体,c、d为导体b内的两点,这两点到点电荷a的距离都等于10cm,当导体b处于静电平衡状态时,导体上的感应电荷在c点和d点产生的电场强度大小分别为Ec=9×106N/C,Ed=9×106N/C.请在图中画出感应电荷在c、d两点产生的电场强度的方向.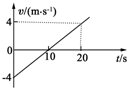 一质点做直线运动,t=0时,位于坐标原点,如图为质点做直线运动的速度-时间图象.由图可知:
一质点做直线运动,t=0时,位于坐标原点,如图为质点做直线运动的速度-时间图象.由图可知: