题目内容
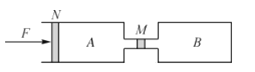
【题目】如图所示，质量M=2kg（含挡板）的长木板静止在足够大的光滑水平面上，其右端挡板固定一劲度系数k=225N/m的水平轻质弹簧，弹簧自然伸长时，其左端到木板左端的距离L=1.6m，小物块（视为质点）以大小v0=10m/s的初速度从木板的左端向右滑上长木板，已知物块的质量m=0.5kg，弹簧的弹性势能Ep=
kx2（其中x为弹簧长度的形变量），弹簧始终在弹性限度内，取g=10m/s2。
(1)若木板上表面光滑，求弹簧被物块压缩后的最大弹性势能Epm；
(2)若木板上表面粗糙，物块与木板间的动摩擦因数μ=0.2，请判断物块是否会压缩弹簧，若物块不会压缩弹簧，求最终物块到木板左端的距离s；若物块会压缩弹簧，求弹簧的最大形变量xm。
【答案】（1）20J；（2）压缩弹簧，最大形变量为0.4m
【解析】
（1）经分析可知，弹簧的弹性势能最大时，物块和木板具有共同速度，设为v，有:
解得:
v=2m/s
根据能量守恒定律有:
解得:
（2）假设物块不会压缩弹簧，且物块在木板上通过的距离为s1，有:
解得:
由于s1＞L，故物块会压缩弹簧，由能量守恒定律有
解得:
练习册系列答案
阅读快车系列答案
相关题目
