题目内容
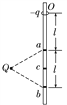
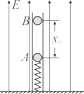
【题目】如图所示,一竖直光滑绝缘的管内有一劲度系数为k的轻质绝缘弹簧,其下端固定于地面,上端与一质量为m、带电量为![]() +q的小球A相连,整个空间存在一竖直向上的匀强电场,小球A静止时弹簧恰为原长,另一质量也为m的不带电的绝缘小球B从管内距A高为x0处由静止开始下落,与A发生碰撞后一起向下运动。若全过程中小球A的电量不发生变化,重力加速度为g。
+q的小球A相连,整个空间存在一竖直向上的匀强电场,小球A静止时弹簧恰为原长,另一质量也为m的不带电的绝缘小球B从管内距A高为x0处由静止开始下落,与A发生碰撞后一起向下运动。若全过程中小球A的电量不发生变化,重力加速度为g。
(1)若x0已知,试求B与A碰撞过程中损失的机械能![]() ;
;
(2)若x0未知,且B与A一起向上运动在最高点时恰未分离,试求A、B运动到最高点时弹簧的形变量x;
(3)在满足第(2)问的情况下,试求A、B运动过程中的最大速度vm。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】解:(1)设匀强电场的场强为E,在碰撞前A静止时有qE=mg ①
解得: ![]()
在与A碰撞前B的速度为v0,由机械能守恒定律得![]() ②
②
![]()
B与A碰撞后共同速度为v1,由动量守恒定律得mv0=2mv1 ③
![]()
B与A碰撞过程中损失的机械能△E为![]() ;
;
(2) A,B在最高点恰不分离,此时A,B加速度相等,且它们间的弹力为零,设此时弹簧的伸长量为x1,则
对B:mg=ma ⑤
对A:mg+kx1-qE=ma ⑥
所以弹簧的伸长量为![]() ;
;
(3) A,B一起运动过程中合外力为零时,具有最大速度vm,设此时弹簧的压缩量为x2,则
2mg-(qE+kx2)=0 ⑦
![]()
由于x1=x2,说明A,B在最高点处与合外力为零处弹簧的弹性势能相等,对此过程由能量守恒定律得
![]()
解得: ![]() 。
。
点晴:解决问题首先要清楚研究对象的运动过程,们要清楚运动过程中能量的转化,以便从能量守恒角度解决问题,把动量守恒和能量守恒结合起来列出等式求解是常见的问题。

练习册系列答案
相关题目