题目内容
16. 倒置的光滑圆锥面内侧,有质量相同的两个小玻璃球A、B,沿锥面在水平面内作匀速圆周运动,关于A、B两球的角速度、线速度和向心加速度正确的说法是( )
倒置的光滑圆锥面内侧,有质量相同的两个小玻璃球A、B,沿锥面在水平面内作匀速圆周运动,关于A、B两球的角速度、线速度和向心加速度正确的说法是( )| A. | 它们的角速度相等ωA=ωB | B. | 它们的线速度υA>υB | ||
| C. | 它们的向心加速度相等 | D. | A球的向心力小于B球的向心力 |
分析 对两小球分别受力分析,求出合力,根据向心力公式和牛顿第二定律列式求解,可得向心加速度、线速度和角速度.
解答 解:对A、B两球分别受力分析,如图
由图可知
F合=F合′=mgtanθ
根据向心力公式有
mgtanθ=ma=mω2R=m$\frac{{v}^{2}}{R}$
解得
a=gtanθ
v=$\sqrt{gRtanθ}$,
$ω=\sqrt{\frac{gtanθ}{R}}$.由于A球转动半径较大,故向心加速度一样大,A球的线速度较大,角速度较小.故B、C正确,A、D错误.
故选:BC.
点评 本题关键受力分析后,求出合力,然后根据向心力公式和牛顿第二定律列式求解.基础题.

练习册系列答案
相关题目
11.利用如图(a)所示电路,可以测量电源的电动势和内阻,所用的实验器材有:
待测电源,电阻箱R(最大阻值999.9Ω),
电阻R0(阻值3.0Ω),电阻R1(阻值3.0Ω),
电流表A(量程为200mA,内阻为RA=6.0Ω),开关S.
实验步骤如下:
①将电阻箱阻值调到最大,闭合开关S;
②多次调节电阻箱,记下电流表的示数I和电阻箱相应的阻值R;
③以$\frac{1}{I}$为纵坐标,R为横坐标,作$\frac{1}{I}$-R图线(用直线拟合)
④求出直线的斜率k和在纵轴上的截距b
回答下列问题:

(1)分别用E和r表示电源的电动势和内阻,则 $\frac{1}{I}$=$\frac{3}{E}$R+$\frac{3}{E}$(5.0+r);.
(2)实验得到的部分数据如表所示,其中电阻R=3.0Ω时电流表的示数如图(b)所示,读出数据,完成表.答:①0.110,②9.09.
(3)在图(c)的坐标纸上将所缺数据点补充完整并作图根据图线求得斜率k=1A-1Ω-1,截距b=6.0A-1.
(4)根据图线求得电源电动势E=3.0V,内阻r=1.0Ω.
待测电源,电阻箱R(最大阻值999.9Ω),
电阻R0(阻值3.0Ω),电阻R1(阻值3.0Ω),
电流表A(量程为200mA,内阻为RA=6.0Ω),开关S.
实验步骤如下:
①将电阻箱阻值调到最大,闭合开关S;
②多次调节电阻箱,记下电流表的示数I和电阻箱相应的阻值R;
③以$\frac{1}{I}$为纵坐标,R为横坐标,作$\frac{1}{I}$-R图线(用直线拟合)
④求出直线的斜率k和在纵轴上的截距b
回答下列问题:

(1)分别用E和r表示电源的电动势和内阻,则 $\frac{1}{I}$=$\frac{3}{E}$R+$\frac{3}{E}$(5.0+r);.
(2)实验得到的部分数据如表所示,其中电阻R=3.0Ω时电流表的示数如图(b)所示,读出数据,完成表.答:①0.110,②9.09.
| R/Ω | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
| I/A | 0.143 | 0.125 | ① | 0.100 | 0.091 | 0.084 | 0.077 |
| I-1/A-1 | 6.99 | 8.00 | ② | 10.0 | 11.0 | 11.9 | 13.0 |
(4)根据图线求得电源电动势E=3.0V,内阻r=1.0Ω.
1.手表的分针长是时针长的2倍,则分针末端线速度与时针末端的线速度之比是( )
| A. | 2:1 | B. | 12:1 | C. | 24:1 | D. | 1:24 |
5.做离心运动的物体,下面说法正确的是( )
| A. | 离心现象是因为向心力小于离心力 | |
| B. | 离心现象是因为合外力不足以提供物体做圆周运动所需向心力 | |
| C. | 速度的大小改变,方向不变 | |
| D. | 速度大小和方向都可能改变 |
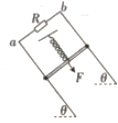 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,导轨电阻不计,上端a,b间接有阻值为R的定值电阻,匀强磁场垂直于导轨平面,磁感应强度的大小为B.质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上,并处于静止状态,现对导体棒施加一个平行于导轨向下的恒力F,导体棒在经过一系列复杂的运动后,最终静止.整个运动过程中导体棒始终与导轨垂直且接触良好,已知弹簧的劲度系数为k,弹簧的重心轴线与导轨ab垂直,重力加速度为g,求:
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,导轨电阻不计,上端a,b间接有阻值为R的定值电阻,匀强磁场垂直于导轨平面,磁感应强度的大小为B.质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上,并处于静止状态,现对导体棒施加一个平行于导轨向下的恒力F,导体棒在经过一系列复杂的运动后,最终静止.整个运动过程中导体棒始终与导轨垂直且接触良好,已知弹簧的劲度系数为k,弹簧的重心轴线与导轨ab垂直,重力加速度为g,求: 如图所示,质量分别为M和m的物块与劲度系数为k的轻质弹簧两端相连,物块M放在地面上,用竖直向下的大小为F的恒力,压在物块m上,直到物块m运动至最低点时撤去恒力,此后物块m将向上运动.已知弹簧的弹性势能与形变量的关系为EP=$\frac{1}{2}$kx2.
如图所示,质量分别为M和m的物块与劲度系数为k的轻质弹簧两端相连,物块M放在地面上,用竖直向下的大小为F的恒力,压在物块m上,直到物块m运动至最低点时撤去恒力,此后物块m将向上运动.已知弹簧的弹性势能与形变量的关系为EP=$\frac{1}{2}$kx2. 某同学在进行“研究平抛物体的运动”实验:
某同学在进行“研究平抛物体的运动”实验: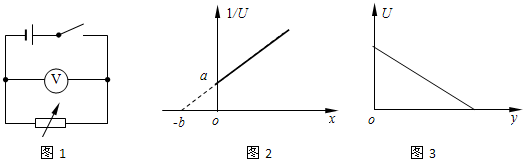
 如图1所示,竖直平面内有不计电阻、宽L=1m的∩型光滑金属框架,其上部分有一个正方形的区域存在随时间变化的匀强磁场B,B-t图如图2所示(垂直框架向里为磁场的正方向).框架下部分有一个虚线所示的区域有垂直框架平面向里的匀强磁场B0=1T,一根质量为m、电阻r=1Ω的金属棒ab跨放框架上与框架接触良好,在第1s内,金属棒恰好能静止.
如图1所示,竖直平面内有不计电阻、宽L=1m的∩型光滑金属框架,其上部分有一个正方形的区域存在随时间变化的匀强磁场B,B-t图如图2所示(垂直框架向里为磁场的正方向).框架下部分有一个虚线所示的区域有垂直框架平面向里的匀强磁场B0=1T,一根质量为m、电阻r=1Ω的金属棒ab跨放框架上与框架接触良好,在第1s内,金属棒恰好能静止.