Question

【题目】半径为R的透明圆柱体处在真空中，如图所示是它的截面图。AB、CD是相互垂直的两条直径，P点与AB距离、Q点与CD距离均为。单色光平行于AB射入透明圆柱体，从A、Q两点射入的光从圆柱体的同一点射出，已知光速为c，求：

（1）该透明圆柱体介质的折射率；

（2）从P点射入的光通过透明圆柱体的时间。

Answer 1

【答案】(1) (2)

【解析】试题分析：作出光路图，由几何关系，结合折射定律，可求该透明圆柱体介质的折射率；由折射定律，结合和几何关系，可求光通过透明圆柱体的时间。

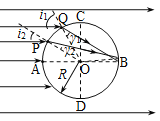
（i）如图所示，设光在Q点的入射角为 ，折射角为 ，在P点的入射角为，折射角为，由几何关系可知

在Q点入射角：

在Q点折射角：

由折射定律有

（2）

在P点入射角：

在P点由折射定律得：