题目内容
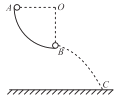
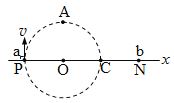
【题目】如图，x为纸面内的一条直线，P、N是x上的两个点，匀强磁场垂直纸面。两个带电粒子a、b分别从P、N同时开始在纸面内运动。a的初速度垂直x向上，运动轨迹如图中虚线所示，O为圆心，PC是直径，A是圆周上的点；b的初速度方向是纸面内所有可能的方向。
已知：AO连线垂直x，PO=OC=CN；a的初速度为v；a、b带等量异种电荷，a的质量为b的两倍，a、b间的相互作用力及所受重力不计。
（1）求a、b的周期之比；
（2）若a、b在A点相遇，求b的速度大小；
（3）b的速度小于某个临界值v0时，a、b不可能相遇，求v0的大小。
【答案】(1) 
(2) 
(3) 
【解析】（1）令a质量为m，电量为q，则b质量为0.5m，电量为-q，设磁感强度为B，
带电粒子在磁场中做圆周运动，由： 
①，
②
可得： 
③；由此求得： 
④
（2）设a、b分别由P、N到A的时间分别为ta、tb，由
⑤； 
⑥
由此可知，a粒子顺时针转了
周时，b粒子逆时针转了半周，也即NA的长度为粒子b做圆周运动的直径。
设a粒子的轨道半径为r； b粒子的速度大小为vb，运动轨道半径为rb。由：
， 
⑦
由几何关系有： 
⑧
联立解得： 
⑨
（3）假设b粒子的速度v’≥v0时，两粒子能在圆周上的Q点相遇，如答图所示，设PQ对应的圆心角为
，
a粒子由P运动到Q点的时间为： 
⑩
b粒子由N运动到Q点的时间为： 
由此可知，b运动到Q的过程中，粒子b转过弧长所对应的圆心角为
，则
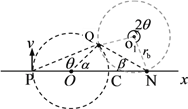
在
中，由正弦定理得： 
得： 
即： 
得： 又：
（当NQ与OQ垂直时取等号）
于是得到： 
；即
练习册系列答案
备战中考寒假系列答案
相关题目
