题目内容
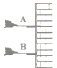
【题目】如图所示,均匀带正电的圆环所带的电荷量为Q,半径为R,圆心为O,A、B、C为垂直于圆环平面且过圆环中心的轴上的三个点,已知BC=2AO=2OB=2R,当在C处放置一点电荷时(不影响圆环的电荷分布情况,整个装置位于真空中),B点的电场强度恰好为零,则由此可得A点的电场强度大小为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
将带电圆环分成若干段,每一小段看作一个点电荷,再根据点电荷场强公式E=k![]() ,求出每个点电荷在B处产生的场强大小。C点处放置一点电荷时,B点的电场强度恰好为零,说明C处点电荷和圆环上的电荷在B处产生的场强大小相等,方向相反,由E=k
,求出每个点电荷在B处产生的场强大小。C点处放置一点电荷时,B点的电场强度恰好为零,说明C处点电荷和圆环上的电荷在B处产生的场强大小相等,方向相反,由E=k![]() 求出C处电荷的带电量。再由电场的叠加原理和对称性求A点的电场强度大小。
求出C处电荷的带电量。再由电场的叠加原理和对称性求A点的电场强度大小。
将圆环等分为n个小段,当n相当大时,每一小段都可以看做点电荷,其所带电荷量为:![]() ;每一点电荷在B处的场强为:
;每一点电荷在B处的场强为:![]() ;由对称性可知,各小段带电环在B处的场强E的垂直于轴向的分量相互抵消,而E1的轴向分量之和即为带电环在B处的场强为:EB=nE1cos45°=
;由对称性可知,各小段带电环在B处的场强E的垂直于轴向的分量相互抵消,而E1的轴向分量之和即为带电环在B处的场强为:EB=nE1cos45°=![]() ;C点处放置一点电荷时,B点的电场强度恰好为零,说明C处点电荷和圆环上的电荷在B处产生的场强大小相等,方向相反,设C处电荷的带电量为q。则有:k
;C点处放置一点电荷时,B点的电场强度恰好为零,说明C处点电荷和圆环上的电荷在B处产生的场强大小相等,方向相反,设C处电荷的带电量为q。则有:k![]() =EB,解得:q=
=EB,解得:q=![]() Q,C处电荷带正电;根据对称性知,圆环在A处的场强大小为:EA1=EB=
Q,C处电荷带正电;根据对称性知,圆环在A处的场强大小为:EA1=EB=![]() ,方向向左。C处电荷在A处产生的场强为:
,方向向左。C处电荷在A处产生的场强为:![]() ,方向向左;所以A点的电场强度大小为:EA=EA1+EA2=
,方向向左;所以A点的电场强度大小为:EA=EA1+EA2=![]() ;故选B。
;故选B。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目