题目内容
【题目】如图所示,一质量为m=1.0×10 -2kg,带电量大小为q=1.0×10 -6C的小球,用绝缘细线悬挂在水平向右的匀强电场中,假设电场足够大,静止时悬线向左与竖直方向成450角。小球在运动过程中电量保持不变,重力加速度g取10m/s2。
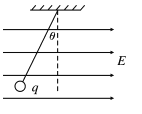
(1)求电场强度E;
(2)若在某时刻将细线突然剪断,求经过1s时小球的位移大小。
【答案】(1)小球带负电,电场强度E为1.7![]() N/C
N/C
(2)细线剪断后1s时小球的速度为20m/s,方向与竖直方向夹角为60°斜向下
【解析】
试题本题的关键是正确对小球受力分析,根据平衡条件可得小球受到的电场力方向向左并可求出电场强度的值,剪断细线后,由于小球受到的重力与电场力都为恒力,所以小球将做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学公式,即可求解.
解:(1)对小球受力分析,受到向下的重力、沿绳子方向的拉力和水平向左的电场力,可见小球应带负电,由平衡条件可得:qE=mgtanθ,解得:E=1.7×![]() N/C.
N/C.
(2)剪断细线后小球做初速度为零的匀加速直线运动,此时小球受到的合力F=![]() ①
①
由牛顿第二定律F=ma可得a=![]() ②
②
又由运动学公式v=at ③
联立以上各式解得:v=20m/s,方向与竖直方向夹角为60°斜向下.
答:(1)小球带负电,电场强度E为1.7![]() N/C
N/C
(2)细线剪断后1s时小球的速度为20m/s,方向与竖直方向夹角为60°斜向下.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目