题目内容
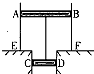
如图,两个侧壁绝热、顶部和底部都导热的相同气缸直立放置,气缸底部和顶部均有细管连通,顶部的细管带有阀门K.两气缸的容积均为V0,气缸中各有一个绝热活塞(质量不同,厚度可忽略).开始时K关闭,两活塞下方和右活塞上方充有气体(可视为理想气体),压强分别为p0和
;左活塞在气缸正中间,其上方为真空;右活塞上方气体体积为
.现使气缸底与一恒温热源接触,平衡后左活塞升至气缸顶部,且与顶部刚好没有接触;然后打开K,经过一段时间,重新达到平衡.已知外界温度为T0,不计活塞与气缸壁间的摩擦.求:
(i)恒温热源的温度T;
(ii)重新达到平衡后左气缸中活塞上方气体的体积Vx.

| p0 |
| 3 |
| V0 |
| 4 |
(i)恒温热源的温度T;
(ii)重新达到平衡后左气缸中活塞上方气体的体积Vx.

(i)与恒温热源接触后,在K未打开时,右活塞不动,两活塞下方的气体经历等压过程,
由盖吕?萨克定律得:
=
①
解得T=
T0②
(ii)由初始状态的力学平衡条件可知,左活塞的质量比右活塞的大.打开K后,左活塞必须升至气缸顶才能满足力学平衡条件.
气缸顶部与外界接触,底部与恒温热源接触,两部分气体各自经历等温过程,设在活塞上方气体压强为p,由玻意耳定律得
PVx=
?
③
对下方气体由玻意耳定律得:(P+P0)(2V0-Vx)=p0?
④
联立③④式得 6VX2-V0VX-V02=0
解得VX=
VX=-
不合题意,舍去.
答:(i)恒温热源的温度T=
T0(ii)重新达到平衡后左气缸中活塞上方气体的体积VX=
由盖吕?萨克定律得:
| T |
| T0 |
| ||
|
解得T=
| 7 |
| 5 |
(ii)由初始状态的力学平衡条件可知,左活塞的质量比右活塞的大.打开K后,左活塞必须升至气缸顶才能满足力学平衡条件.
气缸顶部与外界接触,底部与恒温热源接触,两部分气体各自经历等温过程,设在活塞上方气体压强为p,由玻意耳定律得
PVx=
| P0 |
| 3 |
| V0 |
| 4 |
对下方气体由玻意耳定律得:(P+P0)(2V0-Vx)=p0?
| 7V0 |
| 4 |
联立③④式得 6VX2-V0VX-V02=0
解得VX=
| V0 |
| 2 |
VX=-
| V0 |
| 3 |
答:(i)恒温热源的温度T=
| 7 |
| 5 |
| V0 |
| 2 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目