题目内容
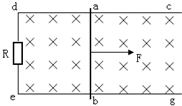 如图所示,固定在水平桌面上的光滑金属杆cdeg处于方向竖直向下的匀强磁场中,金属杆ab接触良好,在端点de之间连接一电阻R,其他部分电阻不计.现用水平向右的力F作用在ab杆上,使金属杆从静止开始做匀加速运动,则能定性表示力F与时间t的关系及线框中感应电流的瞬时功率与位移X的关系的是(以向右为正方向)( )
如图所示,固定在水平桌面上的光滑金属杆cdeg处于方向竖直向下的匀强磁场中,金属杆ab接触良好,在端点de之间连接一电阻R,其他部分电阻不计.现用水平向右的力F作用在ab杆上,使金属杆从静止开始做匀加速运动,则能定性表示力F与时间t的关系及线框中感应电流的瞬时功率与位移X的关系的是(以向右为正方向)( )分析:棒切割磁感线会产生电动势,形成感应电流所以金属杆会受到安培力.当棒处于匀速时棒受力平衡,由已知条件可求出安培力大小,根据受力平衡即可解出金属杆受到的拉力;结合电功率表达式即可找到功率与位移的关系式.
解答:解:设导轨宽度为L,磁场大小为B,金属杆运动的加速度为a,金属杆某时刻的速度为V,
则金属杆受到的安培力为:F安=BIL=B
L ①
由于金属杆从静止开始做匀加速运动,所以某时刻的速度:V=at ②
把②代入①整理:F安=
当棒处于匀速时棒受力平衡,所以拉力F=F安=
,即F与时间t成正比例,故B正确,A错误.
线框中感应电流的瞬时功率:P=I2R═(
)2 R=
=
=
所以功率与位移成正比,故C正确.
故选:BC
则金属杆受到的安培力为:F安=BIL=B
| BLV |
| R |
由于金属杆从静止开始做匀加速运动,所以某时刻的速度:V=at ②
把②代入①整理:F安=
| B2L2at |
| R |
当棒处于匀速时棒受力平衡,所以拉力F=F安=
| B2L2at |
| R |
线框中感应电流的瞬时功率:P=I2R═(
| BLV |
| R |
| B2L2V2 |
| R |
| B2L2(at)2 |
| R |
| 2B2L2ax |
| R |
所以功率与位移成正比,故C正确.
故选:BC
点评:此类题目的解题关键点是能够灵活应用法拉第电磁感应定律与安培力公式,推导出适合图象的表达式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,固定在水平面上的斜面倾角为θ,长方体木块A的质量为M,其PQ面上钉着一枚小钉子,质量为m的光滑小球B通过一细线与小钉子相连接,细线与斜面垂直,以下说法正确的是 (不计空气阻力,重力加速度为g)( )
如图所示,固定在水平面上的斜面倾角为θ,长方体木块A的质量为M,其PQ面上钉着一枚小钉子,质量为m的光滑小球B通过一细线与小钉子相连接,细线与斜面垂直,以下说法正确的是 (不计空气阻力,重力加速度为g)( )| A、若木块匀速下滑,则小球对木块的压力为零 | B、若木块与斜面的动摩擦因数为μ且木块匀速下滑,则小球对木块的压力大小为μmgcosθ | C、若木块与斜面的动摩擦因数为μ且木块匀加速下滑,则小球对木块的压力大小为mgsinθ | D、若斜面光滑,则小球对木块的压力为零 |
 如图所示,固定在水平面上的斜面倾角为θ,长方体木块A质量为M,其PQ面上钉着一枚小钉子,质量为m的小球B通过一细线与小钉子相连接,小球B与PQ面接触,且细线与PQ面平行,木块与斜面间的动摩擦因数为μ.下列说法正确的是( )
如图所示,固定在水平面上的斜面倾角为θ,长方体木块A质量为M,其PQ面上钉着一枚小钉子,质量为m的小球B通过一细线与小钉子相连接,小球B与PQ面接触,且细线与PQ面平行,木块与斜面间的动摩擦因数为μ.下列说法正确的是( ) 如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求:
如图所示,固定在水平地面的倾角为θ斜面上,有一个竖直的挡板,质量为m的光滑圆柱处于静止状态.求: 如图所示,固定在水平桌面上的有缺口的方形木块,abcd为半径为R(已知量)的四分之三圆周的光滑轨道,a为轨道的最高点,de面水平且有足够长度.今将质量为m的小球在d点的正上方某一高度为h(未知量)处由静止释放,让其自由下落到d处切入轨道内运动,小球恰能通过a点,(不计空气阻力,已知重力加速度为g)求:
如图所示,固定在水平桌面上的有缺口的方形木块,abcd为半径为R(已知量)的四分之三圆周的光滑轨道,a为轨道的最高点,de面水平且有足够长度.今将质量为m的小球在d点的正上方某一高度为h(未知量)处由静止释放,让其自由下落到d处切入轨道内运动,小球恰能通过a点,(不计空气阻力,已知重力加速度为g)求: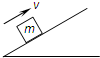 如图所示斜面固定在水平地面上,斜面倾角θ=37°,斜面足够长,物体与斜面间的动摩擦因数μ=0.5.一质量为1kg的物体以v0=4m/s的初速度从斜面底端向上.sin37°=0.6,cos37°=0.8,g取10m/s2,求
如图所示斜面固定在水平地面上,斜面倾角θ=37°,斜面足够长,物体与斜面间的动摩擦因数μ=0.5.一质量为1kg的物体以v0=4m/s的初速度从斜面底端向上.sin37°=0.6,cos37°=0.8,g取10m/s2,求