题目内容
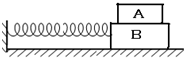 如图所示,A、B质量分别为m和M,B系在固定于墙上的水平轻弹簧的另一端,并置于光滑的水平面上,弹簧的劲度系数为k,将B向右拉离平衡位置x后,无初速度释放,在以后的运动中A、B保持相对静止,求
如图所示,A、B质量分别为m和M,B系在固定于墙上的水平轻弹簧的另一端,并置于光滑的水平面上,弹簧的劲度系数为k,将B向右拉离平衡位置x后,无初速度释放,在以后的运动中A、B保持相对静止,求(1)A在运动中受到的摩擦力最大值为多少.
(2)在从开始到运动
| 1 |
| 4 |
. |
| F |
| F1+F2 |
| 2 |
分析:(1)根据牛顿第二定律求出AB整体的加速度,再以A为研究对象,A所受静摩擦力提供其加速度,当系统加速度最大时,A所受摩擦力最大;
(2)在从开始到运动
周期的过程中,A所受摩擦力由最大变为零,根据:
=
,求出A所受平均摩擦力大小,根据功的定义式即可正确解答.
(2)在从开始到运动
| 1 |
| 4 |
. |
| F |
| F1+F2 |
| 2 |
解答:解:(1)当刚释放时,以整体为研究对象,根据牛顿第二定律得:kx=(M+m)a
此时AB加速度最大为:am=
此时A受摩擦力最大,根据牛顿第二定律得:
fm=mam=
故A在运动中受到的摩擦力最大值为:fm=
.
(2)在
周期时间内,A受,摩擦力线性减小到零,所以根据
=
可知A受到的摩擦力平均值为:
f=
=
则摩擦力对A做的功:
W=f*x=
故在从开始到运动
周期的过程中,摩擦力对A受做功大小为:W=
.
此时AB加速度最大为:am=
| kx |
| m+M |
此时A受摩擦力最大,根据牛顿第二定律得:
fm=mam=
| mkx |
| M+m |
故A在运动中受到的摩擦力最大值为:fm=
| mkx |
| M+m |
(2)在
| 1 |
| 4 |
. |
| F |
| F1+F2 |
| 2 |
f=
| fm |
| 2 |
| mkx |
| 2(M+m) |
则摩擦力对A做的功:
W=f*x=
| mkx |
| 2(M+m) |
故在从开始到运动
| 1 |
| 4 |
| mkx |
| 2(M+m) |
点评:本题考查了牛顿第二定律和求某个力做功等基础知识的应用,注意“整体、隔离”法的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图所示,A.B质量分别为mA=1kg,mB=2kg,A与小车壁的动摩擦因数为0.5,B与小车间的摩擦不计,要使B与小车保持相对静止,求小车的加速度应为多大?(设最大静摩擦力等于滑动摩擦力)
如图所示,A.B质量分别为mA=1kg,mB=2kg,A与小车壁的动摩擦因数为0.5,B与小车间的摩擦不计,要使B与小车保持相对静止,求小车的加速度应为多大?(设最大静摩擦力等于滑动摩擦力) 一颗子弹,质量为m,以初速度v0向右先后击穿放在光滑水平面上靠在一起的A、B两完全相同物体,如图所示,A、B质量均为M,子弹在A、B中所受阻力恒为f,在A内穿行时间为t1,在B内穿行时间为t2,求子弹在A内穿行期间A、B间相互作用力的大小及B的最终速度.
一颗子弹,质量为m,以初速度v0向右先后击穿放在光滑水平面上靠在一起的A、B两完全相同物体,如图所示,A、B质量均为M,子弹在A、B中所受阻力恒为f,在A内穿行时间为t1,在B内穿行时间为t2,求子弹在A内穿行期间A、B间相互作用力的大小及B的最终速度. 如图所示,A、B质量分别为mA和mB,叠放在倾角为θ的斜面上以相同的速度匀速下滑,则( )
如图所示,A、B质量分别为mA和mB,叠放在倾角为θ的斜面上以相同的速度匀速下滑,则( )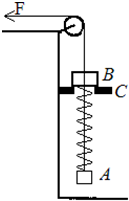 如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用轻质弹簧连接着,弹簧劲度系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面.现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求:
如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用轻质弹簧连接着,弹簧劲度系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面.现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求: