题目内容
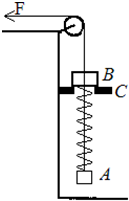 如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用轻质弹簧连接着,弹簧劲度系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面.现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求:
如图所示,A、B质量分别为mA=1kg,mB=2kg,AB间用轻质弹簧连接着,弹簧劲度系数k=100N/m,轻绳一端系在A上,另一端跨过定滑轮,B为套在轻绳上的光滑圆环,另一圆环C固定在桌边,B被C挡住而静止在C上,若开始时作用在绳子另一端的拉力F为零,此时A处于静止且刚没接触地面.现用恒定拉力F=15N拉绳子,恰能使B离开C但不能继续上升,不计摩擦且弹簧没超过弹性限度,求:(1)B刚要离开C时A的加速度;
(2)若把拉力改为F′=30N,则B刚要离开C时,A的加速度和速度.
分析:(1)题中恰能使B离开C但不能继续上升,说明临界情况是弹力等于B的重力,然后对物体A受力分析,根据牛顿第二定律求解加速度;
(2)B刚要离开C时,弹簧的弹力不变,根据牛顿第二定律求解加速度;对两次上拉过程分别运用动能定理列式后联立求解得到速度.
(2)B刚要离开C时,弹簧的弹力不变,根据牛顿第二定律求解加速度;对两次上拉过程分别运用动能定理列式后联立求解得到速度.
解答:解:(1)B刚要离开C的时候,弹簧对B的弹力:N=mBg
A的受力图如图,由图可得:
G+N-F=mAa1
解得:a1=15m/s2,竖直向下
(2)当F=0时,弹簧的伸长量:
X1=
=
=0.1m
当F=15N,且A上升到最高点时,弹簧的压缩量:
X2=
=
=0.2m
所以A上升的高度:
h=X1+X2=0.1+0.2=0.3m
在A上升过程中,根据功能关系:
Fh=mAgh+△Ep
所以弹簧弹性势能增加了:
△Ep=mAgh-Fh=(15-10)×0.3=1.5J
把拉力改为F′=30N,从A上升到当B恰要离开C时的过程中,弹簧的弹性势能变化相等,根据功能关系,有:F′h-mAgh-△Ep=
mA
解得:vA=3m/s
此时,根据牛顿第二定律:
F′-(G+N)=mAa2
解得:a2=0
答:(1)B刚要离开C时A的加速度为5m/s2;
(2)A的加速度为0,速度为3m/s.

A的受力图如图,由图可得:
G+N-F=mAa1
解得:a1=15m/s2,竖直向下
(2)当F=0时,弹簧的伸长量:
X1=
| mAg |
| k |
| 1×10 |
| 100 |
当F=15N,且A上升到最高点时,弹簧的压缩量:
X2=
| mBg |
| k |
| 2×10 |
| 100 |
所以A上升的高度:
h=X1+X2=0.1+0.2=0.3m
在A上升过程中,根据功能关系:
Fh=mAgh+△Ep
所以弹簧弹性势能增加了:
△Ep=mAgh-Fh=(15-10)×0.3=1.5J
把拉力改为F′=30N,从A上升到当B恰要离开C时的过程中,弹簧的弹性势能变化相等,根据功能关系,有:F′h-mAgh-△Ep=
| 1 |
| 2 |
| v | 2 A |
解得:vA=3m/s
此时,根据牛顿第二定律:
F′-(G+N)=mAa2
解得:a2=0
答:(1)B刚要离开C时A的加速度为5m/s2;
(2)A的加速度为0,速度为3m/s.
点评:本题切入点在于“恰能使B离开C但不能继续上升”,然后根据平衡条件和牛顿第二定律列式求解加速度,根据功能关系列式求解末速度.

练习册系列答案
相关题目
 如图所示,A.B质量分别为mA=1kg,mB=2kg,A与小车壁的动摩擦因数为0.5,B与小车间的摩擦不计,要使B与小车保持相对静止,求小车的加速度应为多大?(设最大静摩擦力等于滑动摩擦力)
如图所示,A.B质量分别为mA=1kg,mB=2kg,A与小车壁的动摩擦因数为0.5,B与小车间的摩擦不计,要使B与小车保持相对静止,求小车的加速度应为多大?(设最大静摩擦力等于滑动摩擦力) 一颗子弹,质量为m,以初速度v0向右先后击穿放在光滑水平面上靠在一起的A、B两完全相同物体,如图所示,A、B质量均为M,子弹在A、B中所受阻力恒为f,在A内穿行时间为t1,在B内穿行时间为t2,求子弹在A内穿行期间A、B间相互作用力的大小及B的最终速度.
一颗子弹,质量为m,以初速度v0向右先后击穿放在光滑水平面上靠在一起的A、B两完全相同物体,如图所示,A、B质量均为M,子弹在A、B中所受阻力恒为f,在A内穿行时间为t1,在B内穿行时间为t2,求子弹在A内穿行期间A、B间相互作用力的大小及B的最终速度. 如图所示,A、B质量分别为mA和mB,叠放在倾角为θ的斜面上以相同的速度匀速下滑,则( )
如图所示,A、B质量分别为mA和mB,叠放在倾角为θ的斜面上以相同的速度匀速下滑,则( )