Question

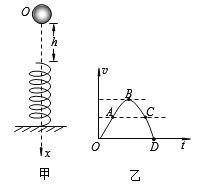
【题目】如图甲所示，劲度系数为k的轻弹簧竖直放置，下端固定在水平地面上，一质量为m的小球，从离弹簧上端高h处由静止释放，落在弹簧上后继续向下运动到最低点的过程中，小球的速度v随时间t的变化图象如图乙所示，其中OA段为直线，AB段是与OA相切于A点的曲线，BCD是平滑的曲线。若以小球开始下落的位置为原点，沿竖直向下方向建立坐标轴Ox，重力加速度为g，则关于A、B、C、D各点对应的小球下落的位置坐标x及所对应的加速度a的大小，以下说法正确的是（ ）

A. xA=h，aA=0

B. xB=h+，aB= 0

C. xC=h+2，aC＞g

D. xD＞h+2，aD＞g

Answer 1

【答案】BD

【解析】试题分析：小球接触弹簧后，构成竖直方向的弹簧振子。OA段是自由落体运动，A的坐标是xA=h，加速度为aA=g，故A错误；小球接触弹簧后，继续向下运动，弹力逐渐增大，小球做加速度减小的加速运动（AB段），速度增加到最大时（B点），加速度减小到零，B点为平衡位置，此时弹力，弹簧压缩量，所以B的坐标，加速度，故B正确；A、C两点速度大小相等，则A、C两点关于B点对称，所以C点弹簧压缩量为，C的坐标，加速度，故C错误；小球由C点继续向下运动到D点，速度减小到零，所以D比C更靠下，D点形变量更大，弹力更大，D的坐标，加速度，故D正确。