题目内容
8. 如图所示,在天花板O的正下方有两点A、B,已知OA=h,AB=H,在天花板上寻找一点C,在点C与A、B之间各连接光滑细线,让两个小球分别穿在细线上,让小球同时从C点下滑,两球同时滑到A、B点,则OC的长度为多少?两球的运动时间为多长?
如图所示,在天花板O的正下方有两点A、B,已知OA=h,AB=H,在天花板上寻找一点C,在点C与A、B之间各连接光滑细线,让两个小球分别穿在细线上,让小球同时从C点下滑,两球同时滑到A、B点,则OC的长度为多少?两球的运动时间为多长?
分析 在点C与A、B之间各连接光滑细线,让两个小球分别穿在细线上,让小球同时从C点下滑,相当于有两个光滑的斜面,小球从斜面上下滑,由受力分析结合牛顿第二定律求得加速度,利用运动学方程求得OC的长度和两球的运动时间.
解答 解:设OC的长度为L,AC、BC与水平面的倾角为α和β,由几何关系可得:
sin$α=\frac{h}{\sqrt{{L}^{2}{+h}^{2}}}$①
sin$β=\frac{h+H}{\sqrt{{L}^{2}{+(h+H)}^{2}}}$②
沿CA和CB方向下滑的小球的加速度分别为:
a1=gsinα,③
a2=gsinβ④
设运动时间为t,由运动学方程可得:$\sqrt{{L}^{2}{+h}^{2}}={\frac{1}{2}}_{\;}$a1t2⑤
$\sqrt{{L}^{2}{+(h+H)}^{2}}=\frac{1}{2}$${{a}_{2}t}^{2}$⑥
解①~⑥可得,L=$\sqrt{\frac{{h(h+H)}^{2}{-h}^{2}(h+H)}{H}}$⑦
联立①③⑤⑦可得,t=$\sqrt{\frac{4h+2H}{g}}$
答:OC的长度为$\sqrt{\frac{{h(h+H)}^{2}{-h}^{2}(h+H)}{H}}$,两球的运动时间为$\sqrt{\frac{4h+2H}{g}}$.
点评 本题采用等效法,将细线轨道转化为斜面模型,将陌生的情景转化为熟悉的情景,利用牛顿第二定律结合运动学方程求解,有一定的运算量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图所示,两个相同的小球A与B分别用一根轻绳和轻弹簧的一端连接,轻绳和轻弹簧的另一端被悬挂在同一高度.现将两个小球都拉至相同的高度,此时弹簧长度为原长,静止释放AB小球运动,当它们运动至最低点时,弹簧与绳长度相等.下列正确的说法是( )
如图所示,两个相同的小球A与B分别用一根轻绳和轻弹簧的一端连接,轻绳和轻弹簧的另一端被悬挂在同一高度.现将两个小球都拉至相同的高度,此时弹簧长度为原长,静止释放AB小球运动,当它们运动至最低点时,弹簧与绳长度相等.下列正确的说法是( )
 如图所示,两个相同的小球A与B分别用一根轻绳和轻弹簧的一端连接,轻绳和轻弹簧的另一端被悬挂在同一高度.现将两个小球都拉至相同的高度,此时弹簧长度为原长,静止释放AB小球运动,当它们运动至最低点时,弹簧与绳长度相等.下列正确的说法是( )
如图所示,两个相同的小球A与B分别用一根轻绳和轻弹簧的一端连接,轻绳和轻弹簧的另一端被悬挂在同一高度.现将两个小球都拉至相同的高度,此时弹簧长度为原长,静止释放AB小球运动,当它们运动至最低点时,弹簧与绳长度相等.下列正确的说法是( )| A. | 两小球运动到各自的最低点时的速度相同 | |
| B. | 与轻绳连接的小球在最低点时的速度较大 | |
| C. | 在运动过程中,小球A的机械能不守恒 | |
| D. | 在运动过程中,小球B的机械能守恒 |
3.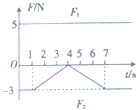 一个质量为m=1kg的物块静止在水平面上,物块与水平面间的动摩擦因数μ=0.2.从t=0时刻起物块同时受到两个水平力F1与F2的作用,若力F1、F2随时间的变化如图所示,设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2,则物块在此后的运动过程中( )
一个质量为m=1kg的物块静止在水平面上,物块与水平面间的动摩擦因数μ=0.2.从t=0时刻起物块同时受到两个水平力F1与F2的作用,若力F1、F2随时间的变化如图所示,设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2,则物块在此后的运动过程中( )
 一个质量为m=1kg的物块静止在水平面上,物块与水平面间的动摩擦因数μ=0.2.从t=0时刻起物块同时受到两个水平力F1与F2的作用,若力F1、F2随时间的变化如图所示,设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2,则物块在此后的运动过程中( )
一个质量为m=1kg的物块静止在水平面上,物块与水平面间的动摩擦因数μ=0.2.从t=0时刻起物块同时受到两个水平力F1与F2的作用,若力F1、F2随时间的变化如图所示,设物块受到的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2,则物块在此后的运动过程中( )| A. | 物块从t=0s起开始运动 | |
| B. | 物块运动后先做加速度运动再做减速运动,最后匀速运动 | |
| C. | 物块加速度的最大值是3m/s2 | |
| D. | 物块在t=4s时速度最大 |
18. 如图所示是某电场中的一条直电场线,一电子从a点由静止释放,它将沿直线向b点运动.下列有关该电场情况的判断正确的是( )
如图所示是某电场中的一条直电场线,一电子从a点由静止释放,它将沿直线向b点运动.下列有关该电场情况的判断正确的是( )
 如图所示是某电场中的一条直电场线,一电子从a点由静止释放,它将沿直线向b点运动.下列有关该电场情况的判断正确的是( )
如图所示是某电场中的一条直电场线,一电子从a点由静止释放,它将沿直线向b点运动.下列有关该电场情况的判断正确的是( )| A. | 该电场一定是匀强电场 | |
| B. | 电场强度一定是Ea<Eb | |
| C. | 电子在a点具有的电势能一定大于在b点的电势能 | |
| D. | 电场中a点的电势一定大于b点的电势 |
 如图,质量为m的小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.物块B置于光滑的水平面上且位于O点正下方,现拉动小球使线水平伸直,小球A由静止开始释放,运动到最低点时与物块B发生正碰(碰撞时间极短,且碰撞过程中无能量损失),已知A和B的质量相等,重力加速度为g.则碰撞后A和B的速度大小分别是0和$\sqrt{2gh}$.
如图,质量为m的小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.物块B置于光滑的水平面上且位于O点正下方,现拉动小球使线水平伸直,小球A由静止开始释放,运动到最低点时与物块B发生正碰(碰撞时间极短,且碰撞过程中无能量损失),已知A和B的质量相等,重力加速度为g.则碰撞后A和B的速度大小分别是0和$\sqrt{2gh}$. 某同学用如图所示的实验装置探究“物块的加速度与力的关系”,他将光电门固定在水平轨道上的B点,用不同质量的重物(用m表示其质量)通过细线拉质量为M的同一物块,每次物块都从同一位置A由静止释放.
某同学用如图所示的实验装置探究“物块的加速度与力的关系”,他将光电门固定在水平轨道上的B点,用不同质量的重物(用m表示其质量)通过细线拉质量为M的同一物块,每次物块都从同一位置A由静止释放.