题目内容
11. 如图,质量为m的小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.物块B置于光滑的水平面上且位于O点正下方,现拉动小球使线水平伸直,小球A由静止开始释放,运动到最低点时与物块B发生正碰(碰撞时间极短,且碰撞过程中无能量损失),已知A和B的质量相等,重力加速度为g.则碰撞后A和B的速度大小分别是0和$\sqrt{2gh}$.
如图,质量为m的小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.物块B置于光滑的水平面上且位于O点正下方,现拉动小球使线水平伸直,小球A由静止开始释放,运动到最低点时与物块B发生正碰(碰撞时间极短,且碰撞过程中无能量损失),已知A和B的质量相等,重力加速度为g.则碰撞后A和B的速度大小分别是0和$\sqrt{2gh}$.
分析 A向下摆动过程机械能守恒,由机械能守恒定律可以求出A到达底端时的速度,
A、B碰撞过程系统动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律可以求出碰撞后A、B的速度.
解答 解:A下摆过程,由机械能守恒定律得:mgh=$\frac{1}{2}$mv2,
解得:v=$\sqrt{2gh}$,
A、B碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:
mv=mvA+mvB,
由机械能守恒定律得:$\frac{1}{2}$mv2=$\frac{1}{2}$mvA2+$\frac{1}{2}$mvB2,
解得:vA=0,vB=$\sqrt{2gh}$;
故答案为:0;$\sqrt{2gh}$.
点评 本题考查了求物体的速度,分析清楚物体运动过程是正确解题的前提与关键,应用机械能守恒定律与动量守恒定律可以解题.

练习册系列答案
相关题目
1.一辆汽车从静止开始做匀加速直线运动,其中第8s内的位移比第5s内的位移多6m,则汽车的加速度以及9s末的速度为( )
| A. | a=3 m/s2 v9=15 m/s | B. | a=1 m/s2 v9=$\frac{17}{3}$ m/s | ||
| C. | a=2 m/s2 v9=14 m/s | D. | a=2 m/s2 v9=18 m/s |
2.下列有关物体运动速度,运动加速度,所受合外力关系的说法正确的是( )
| A. | 物体速度为零时,加速度也为零 | |
| B. | 物体受合外力为零,加速度一定为零 | |
| C. | 物体受合外力为零,速度不一定是零 | |
| D. | 物体加速度变大,速度一定变大 |
6.下列说法中正确的是( )
| A. | 动量守恒定律是由牛顿运动定律推导出来的,所以不能用于研究微观粒子 | |
| B. | 一个氢原子从n=3的激发态跃迁到基态时,最多能辐射3种不同频率的光子 | |
| C. | 天然放射现象的发现揭示了原子核还可再分 | |
| D. | 用γ射线治疗肿瘤时一定要严格控制剂量,以免对人体正常组织造成太大的伤害 |
4.某同学在竖直悬挂的轻弹簧下加挂钩码,做实验研究弹力与弹簧伸长量的关系.下表是该同学的实验数据.实验时弹力始终未超过弹性限度.
(1)根据实验数据填写下表空格
(2)在坐标系中作出弹力F跟弹簧伸长量x关系的图象

(3)根据图象计算弹簧的劲度系数k.(g取10m/s2)
(1)根据实验数据填写下表空格
| 钩码质量m/×10-3kg | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长度L/×10-2m | 6.0 | 7.2 | 8.3 | 9.5 | 10.6 | 11.8 |
| 弹簧伸长量x/×10-2m | 0 | 1.2 | 2.3 | 3.5 | 4.6 | 5.8 |

(3)根据图象计算弹簧的劲度系数k.(g取10m/s2)
9.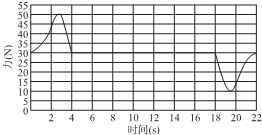 在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
 在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )
在电梯中,把一重物置于水平台秤上,台秤与力的传感器相连,电梯从静止开始一直上升,最后停止运动:传感器的屏幕上显示出其所受的压力与时间的关系(FN一t)图象,如图所示,则下列说法中正确的是( )| A. | 0~4s电梯中的物体处于超重状态 | |
| B. | 18~22s内,电梯中的物体处于先超重再失重状态 | |
| C. | 从图中可以求出物体的重力 | |
| D. | 从图中可以找出电梯上升时最大加速度 |
 根据玻尔原子结构理论,氦离子(He+)的能级图如图所示.电子处在n=3轨道上比处在n=5轨道上离氦核的距离近 (选填“近”或“远”). 当大量He+处在n=5的激发态时,由于跃迁所发射的谱线共有10条.
根据玻尔原子结构理论,氦离子(He+)的能级图如图所示.电子处在n=3轨道上比处在n=5轨道上离氦核的距离近 (选填“近”或“远”). 当大量He+处在n=5的激发态时,由于跃迁所发射的谱线共有10条. 如图所示,在天花板O的正下方有两点A、B,已知OA=h,AB=H,在天花板上寻找一点C,在点C与A、B之间各连接光滑细线,让两个小球分别穿在细线上,让小球同时从C点下滑,两球同时滑到A、B点,则OC的长度为多少?两球的运动时间为多长?
如图所示,在天花板O的正下方有两点A、B,已知OA=h,AB=H,在天花板上寻找一点C,在点C与A、B之间各连接光滑细线,让两个小球分别穿在细线上,让小球同时从C点下滑,两球同时滑到A、B点,则OC的长度为多少?两球的运动时间为多长?