题目内容
13. 某同学用如图所示的实验装置探究“物块的加速度与力的关系”,他将光电门固定在水平轨道上的B点,用不同质量的重物(用m表示其质量)通过细线拉质量为M的同一物块,每次物块都从同一位置A由静止释放.
某同学用如图所示的实验装置探究“物块的加速度与力的关系”,他将光电门固定在水平轨道上的B点,用不同质量的重物(用m表示其质量)通过细线拉质量为M的同一物块,每次物块都从同一位置A由静止释放.(1)若用游标卡尺测出遮光条的宽度为d,由数字计时器读出遮光条通过光电门的时间为△t,则物块经过光电门时的速度为 $\frac{d}{△t}$(用所给物理量的符号表示).
(2)若测得AB间的距离为s,则结合(1)可得物块的加速度a=$\frac{{d}^{2}}{2s△{t}^{2}}$(用所给物理量的符号表示),细线对物块的拉力F与mg的关系为F<mg(选填“>”“=”或“<”).
分析 (1)由于遮光条通过光电门的时间极短,可以用平均速度表示瞬时速度.
(2)由题意可知,该实验中保持小车质量M不变,根据运动学公式和牛顿第二定律表示出变量之间的关系求解.
解答 解:(1)由于遮光条通过光电门的时间极短,可以用平均速度表示瞬时速度v=$\frac{d}{△t}$;
(2)由题意可知,该实验中保持小车质量M不变,因此有:v2=2as,a=$\frac{{v}^{2}}{2s}=\frac{{d}^{2}}{2s△{t}^{2}}$,
而a=$\frac{F}{M}$=$\frac{mg}{M}$,
而实际的操作中,小物块的重力提供小车与小物块共同的加速度,即:$a′=\frac{mg}{m+M}$,此时的拉力:$F=Ma′=\frac{Mmg}{m+M}<mg$;
故答案为:(1)$\frac{d}{△t}$;(2)$\frac{{d}^{2}}{2s△{t}^{2}}$,<
点评 该题考查加速度的测量,处理实验时一定要找出实验原理,根据实验原理我们可以寻找需要测量的物理量和需要注意的事项.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
4.某同学在竖直悬挂的轻弹簧下加挂钩码,做实验研究弹力与弹簧伸长量的关系.下表是该同学的实验数据.实验时弹力始终未超过弹性限度.
(1)根据实验数据填写下表空格
(2)在坐标系中作出弹力F跟弹簧伸长量x关系的图象

(3)根据图象计算弹簧的劲度系数k.(g取10m/s2)
(1)根据实验数据填写下表空格
| 钩码质量m/×10-3kg | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长度L/×10-2m | 6.0 | 7.2 | 8.3 | 9.5 | 10.6 | 11.8 |
| 弹簧伸长量x/×10-2m | 0 | 1.2 | 2.3 | 3.5 | 4.6 | 5.8 |

(3)根据图象计算弹簧的劲度系数k.(g取10m/s2)
1. 如图所示,物体A叠放在物体B上,物体B置于光滑水平面上,物体A、B的质量分别为mA=6kg、mB=2kg,物体A、B间的动摩擦因数μ=0.2.开始时水平力F作用在物体A上且F=10N,此后逐渐增大F,在增大到45N的过程中(g取10m/s2)( )
如图所示,物体A叠放在物体B上,物体B置于光滑水平面上,物体A、B的质量分别为mA=6kg、mB=2kg,物体A、B间的动摩擦因数μ=0.2.开始时水平力F作用在物体A上且F=10N,此后逐渐增大F,在增大到45N的过程中(g取10m/s2)( )
 如图所示,物体A叠放在物体B上,物体B置于光滑水平面上,物体A、B的质量分别为mA=6kg、mB=2kg,物体A、B间的动摩擦因数μ=0.2.开始时水平力F作用在物体A上且F=10N,此后逐渐增大F,在增大到45N的过程中(g取10m/s2)( )
如图所示,物体A叠放在物体B上,物体B置于光滑水平面上,物体A、B的质量分别为mA=6kg、mB=2kg,物体A、B间的动摩擦因数μ=0.2.开始时水平力F作用在物体A上且F=10N,此后逐渐增大F,在增大到45N的过程中(g取10m/s2)( )| A. | 当力F<12 N时,两物体均保持静止状态 | |
| B. | 两物体始终没有相对运动 | |
| C. | 两物体从受力开始就有相对运动 | |
| D. | 两物体开始没有相对运动,当拉力超过12 N时,开始相对滑动 |
3.已知下面的哪组数据,可以计算出地球的质量M地(只知引力常量G)( )
| A. | 地球表面的重力加速g和地球的半径R | |
| B. | 月球绕地球运动的周期T1及地球的半径R | |
| C. | 地球绕太阳运动的周期T2及地球到太阳中心的距离R2 | |
| D. | 地球“同步卫星”离地面的高度h |
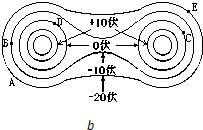 如图所示,是一组两个平行带电圆柱垂直平面的等势线,在图中标出了各等势线的电势数值.试求:
如图所示,是一组两个平行带电圆柱垂直平面的等势线,在图中标出了各等势线的电势数值.试求: 如图所示,在天花板O的正下方有两点A、B,已知OA=h,AB=H,在天花板上寻找一点C,在点C与A、B之间各连接光滑细线,让两个小球分别穿在细线上,让小球同时从C点下滑,两球同时滑到A、B点,则OC的长度为多少?两球的运动时间为多长?
如图所示,在天花板O的正下方有两点A、B,已知OA=h,AB=H,在天花板上寻找一点C,在点C与A、B之间各连接光滑细线,让两个小球分别穿在细线上,让小球同时从C点下滑,两球同时滑到A、B点,则OC的长度为多少?两球的运动时间为多长? (1)在测量某合金丝的电阻率实验中,用螺旋测微器测量该合金丝的直径,用米尺测量合金丝的长度,其中电流表、电压表的读数如图甲所示.由图可以读出合金丝两端的电压U=2.15V,流过合金丝的电流强度I=0.44A,由图乙读出合金丝的长度l=30.50cm,由图丙读出合金丝的直径d=0.200mm;
(1)在测量某合金丝的电阻率实验中,用螺旋测微器测量该合金丝的直径,用米尺测量合金丝的长度,其中电流表、电压表的读数如图甲所示.由图可以读出合金丝两端的电压U=2.15V,流过合金丝的电流强度I=0.44A,由图乙读出合金丝的长度l=30.50cm,由图丙读出合金丝的直径d=0.200mm; 如图所示在竖直放置的两块足够长的平行金属板间有匀强电场.其电场强度为E,在该
如图所示在竖直放置的两块足够长的平行金属板间有匀强电场.其电场强度为E,在该