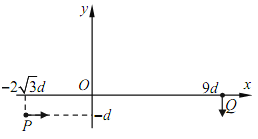题目内容
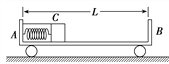
【题目】如图所示，小车停放在光滑的水平面上，小车的质量为M= 8kg,在小车水平面A处放有质量为m=2kg的物块，AB段是粗糙的水平面，BC是一段光滑的圆弧，在B点处与AB相切，现给物块一个v0=5m/s的初速度，物块便沿AB滑行，并沿BC上升，然后又能返回，最后恰好回到A点处与小车保持相对静止，求：
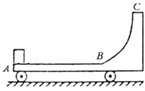
（1）从物块开始滑动至返回A点整个过程中,小车与物块组成的系统损失的机械能为多少?
（2）物块沿BC弧上升相对AB平面的最大高度为多少?
【答案】（1）
（2）h=0.5m
【解析】试题分析：①物体返回A点时与小车相对静止设它们速度为V1则：
（ 2分）
（2分）
解得：（1分）
②设最高点时两物体速度为V2，高度为h，物体从A到最高点的过程中：
（1分）
（2分）
解得：h=0.5m （1分）
考点：本题考查动量守恒定律和能量守恒定律。
【题型】解答题
【结束】
109
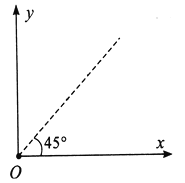
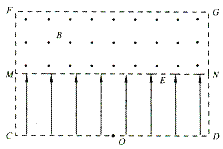
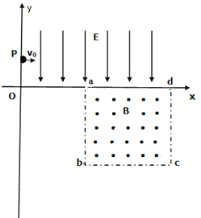
【题目】如图所示的平面直角坐标系xOy，在第一象限内有平行于y轴的匀强电场，方向沿y轴负方向；在第四象限的正方形abcd区域内有匀强磁场，方向垂直于xOy平面向外，正方形边长为L，且ab边与y轴平行。一质量为m、电荷量为q的粒子，从y轴上的P（0，h）点，以大小为v0的速度沿x轴正方向射入电场，通过电场后从x轴上的a（2h,0）点进入第四象限，又经过磁场从y轴上的某点进入第三象限，且速度与y轴负方向成45°角，不计粒子所受的重力。求：
（1）判断粒子带电的电性，并求电场强度E的大小；
（2）粒子到达a点时速度的大小和方向；
（3）abcd区域内磁场的磁感应强度B的最小值。
【答案】（1）粒子带正电 
（2）
45° （3）
【解析】
试题分析： （1） 粒子带正电 （1分）
设粒子在电场中运动的时间为t，则有
（2分）
， （2分）
（2分）
联立以上各式可得
（1分）
（2）粒子到达a点时沿y轴方向的分速度
（2分）
所以
， （2分）
方向指向第Ⅳ象限与x轴正方向成45°角。 （1分）
（3）粒子在磁场中运动时，有
（2分）
当粒子从b点射出时，磁场的磁感应强度为最小值，
此时有
，（2分）
所以
（1分）
