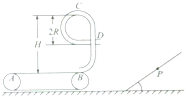
[题目]如图所示.在光滑水平冰面上.一蹲在滑板上的小孩推着冰车一起以速度v0＝1.0m/s向左匀速运动．某时刻小孩将冰车以相对冰面的速度v1＝7.0m/s向左推出.冰车与竖直墙发生碰撞后原速率弹回．已知冰车的质量为m1＝10kg.小孩与滑板的总质量为m2＝30kg.小孩与滑板始终无相对运动．取g＝10m/s2.①求冰车与竖直墙发题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，在光滑水平冰面上，一蹲在滑板上的小孩推着冰车一起以速度v0＝1.0m/s向左匀速运动．某时刻小孩将冰车以相对冰面的速度v1＝7.0m/s向左推出，冰车与竖直墙发生碰撞后原速率弹回．已知冰车的质量为m1＝10kg，小孩与滑板的总质量为m2＝30kg，小孩与滑板始终无相对运动．取g＝10m/s2.

①求冰车与竖直墙发生碰撞过程中，墙对冰车的冲量大小I；

②通过计算判断，冰车能否追上小孩？

【答案】(1) (2) 冰车能追上小孩

【解析】试题分析：根据动量定理可得墙对冰车的冲量大小I；根据动量守恒定律求出小孩推出冰车后与滑板共同运动的速度为v，在与木块的速度相比较即可解题。

①冰车在碰撞过程由动量定理有

解得

②设小孩推出冰车后与滑板共同运动的速度为v，由动量守恒定律有

解得

由于，故冰车能追上小孩

练习册系列答案

期末满分冲刺阶段练习与单元测试系列答案

轻松15分导学案系列答案

相关题目

【题目】测定电阻的阻值，实验室提供下列器材：

A．待测电阻R(阻值约10kΩ) B．滑动变阻器R1(0-lkΩ)

C．电阻箱Ro(99999.9Ω) D．灵敏电流计G(500A，内阻不可忽略)

E．电压表V(3V，内阻约3kΩ) F．直流电源E(3V，内阻不计)

G．开关、导线若干

(1)甲同学设计了如图a所示的电路，请你指出他的设计中存在的问题：

①___________；②___________；③___________

(2)乙同学用图b所示的电路进行实验.

①请在图d中用笔画线代替导线，完成实物电路的连接_______.

②先将滑动变阻器的滑动头移到_____(选填“左”或“右”)端，再接通开关S；保持S2断开，闭合S1，调节R1使电流计指针偏转至某一位置，并记下电流I1

③断开S1，保持R1不变，调整电阻箱R0阻值在10kΩ左右，再闭合S2，调节R0阻值使得电流计读数为________时，R0的读数即为电阻的阻值.

(3)丙同学查得灵敏电流计的内阻为Rg，采用电路c进行实验，改变电阻箱电阻R0值，读出电流计相应的电流I，由测得的数据作出-R0图象如图e所示，图线纵轴截距为m，斜率为k，则电阻的阻值为________________

【题目】能源是社会发展的基础，发展核能是解决能源问题的途径之一，核能作为一种新能源在现代社会中已不可缺少，我国在完善核电安全基础上将加大核电站建设规模，核泄漏中的钚（Pu）是一种具有放射性的超铀元素，它可破坏细胞基因，提高罹患癌症的风险，已知钚的一种同位素的半衰期为24100年，其衰变方程为，下列有关说法正确的是

A. X原子核中含有92个中子

B. 100个经过24100年后一定还剩余50个

C. 由于衰变时释放巨大的能量，根据，衰变过程总质量增加

D. 衰变发出的射线是波长很短的光子，具有很强的穿透能力

【题目】如图所示，水平传送带的右端与竖直面内的用光滑钢管弯成的“9“形固定轨道相接，钢管内径很小．传送带的运行速度为v0=6m/s，将质量m=1.0kg的可看作质点的滑块无初速地放到传送带A端，传送带长度为L=12.0m，“9“字全高H=0.8m．“9“字上半部分圆弧半径为R=0.2m，滑块与传送带间的动摩擦因数为μ=0.3，重力加速度g=10m/s2，试求：

（1）滑块从传送带A 端运动到B端所需要的时间；

（2）滑块滑到轨道最高点C时对轨道作用力的大小和方向；

（3）若滑块从“9”形轨道D点水平抛出后，恰好垂直撞在倾角θ=45°的斜面上P点，求P、D两点间的竖直高度h．

【题目】如图所示，小车停放在光滑的水平面上，小车的质量为M= 8kg,在小车水平面A处放有质量为m=2kg的物块，AB段是粗糙的水平面，BC是一段光滑的圆弧，在B点处与AB相切，现给物块一个v0=5m/s的初速度，物块便沿AB滑行，并沿BC上升，然后又能返回，最后恰好回到A点处与小车保持相对静止，求：