��Ŀ����
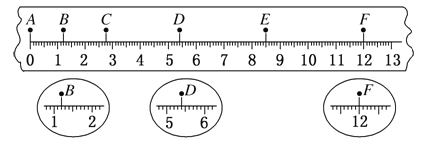
����Ŀ����ͼ��ʾ���ھ�������CDNM������ֽ�����ϵ���ǿ�糡����ǿ�Ĵ�СE=1��5��105 V/m���ھ�������MNGF���д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СB=0��2 T����֪CD=MN=FG=0��60 m��CM=MF=0��20 m����CD���е�O����һ����Դ����ֽ����糡�и�������ȵط�������ʾ�Ϊv0=1��0��106 m/s��ij�ִ��������ӣ���������m=6��4��10-27 kg�������q=3��2��10-19 C�����ӿ������谭��ͨ���߽�MN����ų����������ӵ���������
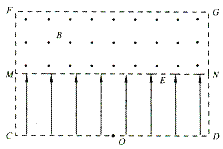
��1�������ڴų�����Բ���˶��İ뾶��
��2���߽�FG������������ų��ķ�Χ���ȣ�
��3�������ڴų����˶����ʱ�䣮�������ʽ��������λ��Ч���֣�
���𰸡���1��0��2 m��2��0��43 m��3��2��1��10-7 s
��������
�����������1���糡���ɶ��ܶ����ã�![]()
������֪![]() ���������ݵ�
���������ݵ�
v=2��106 m/s
���������ڴų���������Բ���˶���![]() �����
�����![]() ��
��
��2���������ش�ֱ�ڵ糡��������ʱ�����糡ʱˮƽλ��Ϊx������ƽ���ɵã�![]()
���![]()
�뿪�糡ʱ�����ٶ���ˮƽ�ٶȵļн���![]() ��
��
�������֪��PS��MN����OC����������ӵ���P�㣬Ϊ��߽磬��ֱMN�����������߽�FG������Q�㣬QΪ�ұ߽磬QO��=r���켣��ͼ��
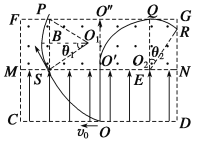
��Χ����Ϊ![]() ��
��
��3���������ڹ�ʽ![]() ���ɷ�����֪��OO�䷽������������˶�ʱ�������FG����ΪL
���ɷ�����֪��OO�䷽������������˶�ʱ�������FG����ΪL
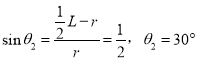
���������ڴų����˶������Բ�Ľ�Ϊ120�㣬��Ӧ���ʱ��Ϊ![]()

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�