Question

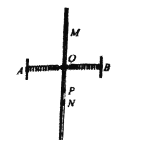
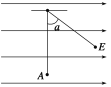
【题目】如图所示，一条长为L的细线上端固定，下端拴一个质量为m的电荷量为q的小球，将它置于方向水平向右的匀强电场中，使细线竖直拉直时将小球从A点静止释放，当细线离开竖直位置偏角α＝60°时，小球速度为零.

(1)求：①小球带电性质；②电场强度E.

(2)若小球恰好完成竖直圆周运动，求从A点释放小球时应有的初速度vA的大小(可含根式)．

Answer 1

【答案】（1）正电， （2）

【解析】

(1) 小球在电场中受到重力、电场力和细线的拉力而处于平衡状态。根据细线偏离的方向，分析电场力方向，确定小球的电性。根据平衡条件和电场力公式F=qE，列方程求出电场强度；

(2) 根据题意可知，由力的平行四边形定则求出电场力与重力的合力，可等效成新的重力，小球若能以最小速度通过新重力的对应的最高点，则小球恰好完成竖直圆周运动，从而根据动能定理，可求出A点释放小球时应有初速度的大小。

(1) 由图可知，小球所受电场力方向水平向右，场强也水平向右，则小球带正电

由题意可知，细线离开竖直位置偏角的角平分线的位置，即为小球平衡位置

解得：；

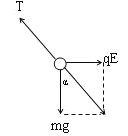
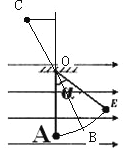
(2) 小球除拉力外，还受到电场力与重力作用，由于其两个不变，因此可等效成新的重力，所以要小球恰好完成竖直圆周运动，则小球必须能以最小速度通过新的重力对应的最高点

由牛顿第二定律有：

从而A点到新的重力对应的最高点C，根据动能定理得，

由以上两式解得： 。