题目内容
【题目】(20分)对铀235的进一步研究在核能的开发和利用中具有重要意义。如图所示,质量为m、电荷量为q的铀235离子,从容器A下方的小孔S1不断飘入加速电场,其初速度可视为零,然后经过小孔S2垂直于磁场方向进入磁感应强度为B的匀强磁场中,做半径为R的匀速圆周运动。离子行进半个圆周后离开磁场并被收集,离开磁场时离子束的等效电流为I。不考虑离子重力及离子间的相互作用。
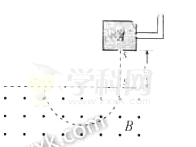
(1)求加速电场的电压U;
(2)求出在离子被收集的过程中任意时间t内收集到离子的质量M;
(3)实际上加速电压的大小会在U+ΔU范围内微小变化。若容器A中有电荷量相同的铀235和铀238两种离子,如前述情况它们经电场加速后进入磁场中会发生分离,为使这两种离子在磁场中运动的轨迹不发生交叠,![]() 应小于多少?(结果用百分数表示,保留两位有效数字)
应小于多少?(结果用百分数表示,保留两位有效数字)
【答案】(1)![]() (2)
(2)![]() (3)0.63%
(3)0.63%
【解析】解:(1)设离子经电场加速后进入磁场时的速度为v,由动能定理得:
qU =![]() mv2
mv2
离子在磁场中做匀速圆周运动,由牛顿第二定律得:
qvB=![]()
解得:U =![]()
(2)设在t时间内收集到的离子个数为N,总电荷量Q = It
Q = Nq
M =" Nm" =![]()
(3)由以上分析可得:R =![]()
设m/为铀238离子质量,由于电压在U±ΔU之间有微小变化,铀235离子在磁场中最大半径为:Rmax=![]()
铀238离子在磁场中最小半径为:Rmin=![]()
这两种离子在磁场中运动的轨迹不发生交叠的条件为:Rmax<Rmin
即:![]() <
<![]()
得:![]() <
<![]()
![]() <
<![]()
其中铀235离子的质量m = 235u(u为原子质量单位),铀238离子的质量m,= 238u
则:![]() <
<![]()
解得:![]() <0.63%
<0.63%

练习册系列答案
相关题目