题目内容
【题目】如图所示,在平面直角坐标系xOy的第一象限内存在垂直于坐标平面的匀强磁场(未画出),第二象限存在水平向左的匀强电场。质量为m、电荷量为-q的带电粒子从第三象限无初速度释放后,经电压为U的电场加速后从P(![]() ,0)点垂直x轴进入第二象限,然后从A(0,2L)点进入第一象限,又经磁场偏转后垂直x轴进入第四象限。不计粒子重力。
,0)点垂直x轴进入第二象限,然后从A(0,2L)点进入第一象限,又经磁场偏转后垂直x轴进入第四象限。不计粒子重力。
(1)求第二象限内电场强度的大小;
(2)若第一象限内的磁场方向垂直于坐标平面向里,求磁场的磁感应强度大小;
(3)若第一象限某矩形区域内存在匀强磁场,磁场方向垂直于坐标平面向外,磁感应强度大小取第(2)问计算结果,求矩形区域的最小面积。

【答案】(1)![]() ;(2)
;(2)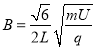 ;(3)
;(3)![]()
【解析】
(1)设粒子从P点进入电场的速度大小为v0,根据动能定理有
![]()
粒子进入电场后做类平抛运动,有
水平方向
![]()
竖直方向有
2L=v0t
其中
![]()
联立解得
![]()
(2)粒子进入第一象限的匀强磁场后,做匀速圆周运动,如图所示
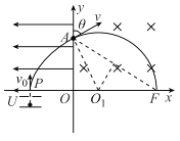
由![]() 得
得
![]()
解得
![]() =60°
=60°
则粒子进入磁场中的速度为
![]()
设粒子在磁场中做圆周运动的半径为r,则有
![]()
解得
![]()
由洛伦兹力提供向心力得
![]()
联立解得
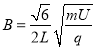
(3)磁感应强度大小不变,粒子做匀速圆周运动的半径大小不变,即
![]()
画出粒子轨迹示意图如图所示
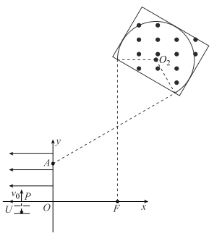
由几何关系可知粒子偏转240°,所以
矩形的长边为
![]()
宽边为
![]()
则最小面积为
![]()

【题目】著名的物理学家密立根以精湛的技术测量光电效应中金属的遏止电压Uc与入射光的额率v,由此求出普朗克常量h。下表是他在一次实验中测得某金属的Uc和v的几组数据,现已根据表中数据做出Uc-v图象如图所示,试由图象求出:
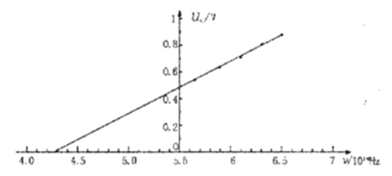
Uc/V | 0.541 | 0.637 | 0.714 | 0.809 | 0.878 |
v/ | 5.644 | 5.888 | 6.098 | 6.303 | 6.501 |
(1)这种金属的截止频率____________________Hz;(保留三位有效数字)
(2)普朗克常量_______________J·s。(保留两位有效数字)(已知元电荷:![]() C)
C)