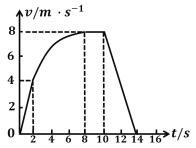��Ŀ����
����Ŀ������Ϊ�ʵ��С����Ӱ뾶Ϊ0.8m���ķ�֮һ�⻬Բ��������˻��¡��ڹ����͵㻬��ˮƽ���ʹ������Ҷˣ������νӴ���е����ʧ�����贫�ʹ�����L=8m�����Ժ㶨��v=3m/s�ٶ�˳ʱ��ת����С����ǡ�����˶���ˮƽ���ʹ�������˶�û�е��´��ʹ�����֪�������ٶȴ�СΪg=10m/s2����

��1������봫�ʹ���Ķ�Ħ��������
��2������Բ�������͵㻬�봫�ʹ�����һ�η���Բ�������͵����õ�ʱ�䣨��С�������������λ��Ч���֣���
���𰸡���1��0.1����2��8.17s
��������
��1������Բ�ι⻬����»��Ĺ��̣����ݻ�е���غ���
![]()
���![]()
����ش��ʹ�����������ٶ�ǡ��Ϊ�㣬�ɶ��ܶ�����![]()
�������ݽ�ã�![]()
��2������ڴ��ʹ������ȼ����˶�![]()
�������ٵ����ʱ��Ϊ![]()
�������ʱ���ٶȲ��䣬�ʼ���ʱ��Ϊ![]()
���ʱ���λ��Ϊ![]()
֮������洫�ʹ������˶�����![]()
����ڴ��ʹ��ϵ�һ���������õ�ʱ��Ϊ![]()

��ϰ��ϵ�д�
�����Ŀ