题目内容
【题目】已知某船在静水中的速率为v1=4 m/s,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽为d=100 m,河水的流动速度为v2=3 m/s,方向与河岸平行.试分析:
(1)欲使船以最短时间渡过河船发生的位移是多大?
(2)欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?
(3)若水速变成v3=5 m/s,其余条件不变,欲使船渡河过程中的航行距离最短,船的航向又应怎样?渡河所用时间是多少?
【答案】(1) ![]() ,L=125m;(2)
,L=125m;(2) ![]() ,
, ![]() ;(3)
;(3) ![]() ,t=41.7s
,t=41.7s
【解析】(1)当船头垂直对岸行到对岸时,所需要的时间最短,最短时间为: ![]()
船沿着水流方向的位移大小:s=vst=3×25=75m;
船发生的位移是: ![]() ;
;
(2)欲使船航行距离最短,需使船的实际位移(合位移)与河岸垂直,如左图: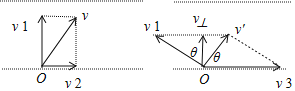
则船的合速度为: ![]() ,
, ![]() ;
;![]() ;即船头指向与河对岸的夹角为
;即船头指向与河对岸的夹角为![]()
(3)若河水的流动速度增大为v3=5m/s,此时水的速度大于船的速度时,船不能垂直于河岸到达对岸,当船速与合速度的方向垂直时,即合速度的方向与河岸之间的夹角最大时,船渡河过程中的航行距离最短.如右图;
此时垂直于河岸方向的分速度:v⊥=1cosθ
又: ![]()
渡河的时间:t′=![]()
代入数据联立得:t′=41.7s

练习册系列答案
相关题目