题目内容
【题目】如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合。转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°。重力加速度大小为g。

(1)若ω=ω0,小物块受到的摩擦力恰好为零,求ω0;
(2)ω=(1±k)ω0,且0<k <<1,求小物块受到的摩擦力大小和方向。
【答案】(1)![]()
(2)当![]() 时,摩擦力方向沿罐壁切线向下,大小为
时,摩擦力方向沿罐壁切线向下,大小为![]() ;当
;当![]() 时,摩擦力方向沿罐壁切线向下,大小为
时,摩擦力方向沿罐壁切线向下,大小为![]() ;
;
【解析】(1)物块随陶罐在水平面内做匀速圆周运动,当物块受到的摩擦力恰好等于零时,物块受到的重力和陶罐对其施加的指向O点的支持力的合力提供向心力,有![]() ,代入数据,可得,
,代入数据,可得,![]() 。
。
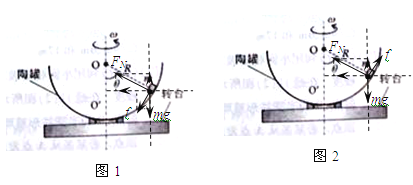
(2)当![]() 时,物块受到的摩擦力沿陶罐壁切线向下,设摩擦力的大小为f,陶罐壁对物块的支持力为FN,对物块受力分析,如图1所示,则:
时,物块受到的摩擦力沿陶罐壁切线向下,设摩擦力的大小为f,陶罐壁对物块的支持力为FN,对物块受力分析,如图1所示,则:
水平方向:![]() ;竖直方向:
;竖直方向:![]()
代入数据,解得:![]() (2分)
(2分)
同理,当![]() 时,物块受到的摩擦力沿陶罐壁切线向上,对其受力分析,如图2所示,则:
时,物块受到的摩擦力沿陶罐壁切线向上,对其受力分析,如图2所示,则:
水平方向:![]() ;竖直方向:
;竖直方向:![]()
代入数据,解得:![]()

 黄冈创优卷系列答案
黄冈创优卷系列答案【题目】(1)在做“用单摆测定重力加速度”的实验中,某同学甲用毫米刻度尺测得摆线长![]() ;用游标卡尺测得摆球的直径如图所示,则摆球直径
;用游标卡尺测得摆球的直径如图所示,则摆球直径![]() ____________
____________![]() .
.
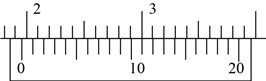
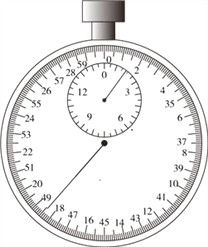
用秒表测得单摆完成![]() 次全振动的时间如图所示,则秒表的示数
次全振动的时间如图所示,则秒表的示数![]() ____________
____________![]() ;若用给出的各物理量符号(L0、
;若用给出的各物理量符号(L0、![]() 、
、![]() 、
、![]() )表示当地的重力加速度
)表示当地的重力加速度![]() ,则计算
,则计算![]() 的表达式为
的表达式为![]() ____________.
____________.
(2)实验中同学甲发现测得的![]() 值偏小,可能的原因是_______
值偏小,可能的原因是_______
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将![]() 次全振动计为
次全振动计为![]() 次
次
(3)为了提高实验精度,某同学乙在实验中通过改变几次摆长![]() ,并测出相应的周期
,并测出相应的周期![]() ,从而得到一组对应的
,从而得到一组对应的![]() 与
与![]() 的数据,再以
的数据,再以![]() 为横坐标、
为横坐标、![]() 为纵坐标,建立坐标系,将所得数据进行连线,实验测得的数据如下表所示:
为纵坐标,建立坐标系,将所得数据进行连线,实验测得的数据如下表所示:
次数 |
|
|
|
|
|
摆长 |
|
|
|
|
|
|
|
|
|
|
|
振动周期 |
|
|
|
|
|
振动周期的平方 |
|
|
|
|
|
请将表中第三次测量数据标在右图中,并在右图中作出![]() 随
随![]() 变化的关系图象__________.
变化的关系图象__________.
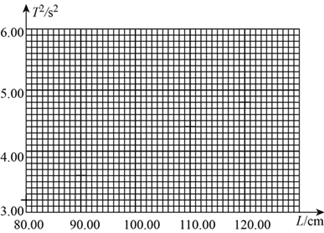
②根据图象,可知当地的重力加速度为____________(保留![]() 位有效数字).
位有效数字).





