题目内容
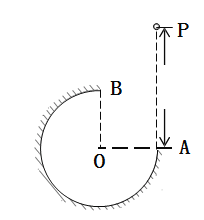
【题目】如图所示为演示“过山车”原理的实验装置，该装置由两段倾斜直轨道与一圆轨道拼接组成，在圆轨道最低点处的两侧稍错开一段距离，并分别与左右两侧的直轨道平滑相连。
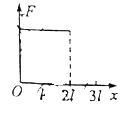
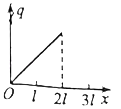
某研学小组将这套装置固定在水平桌面上，然后在圆轨道最高点A的内侧安装一个薄片式压力传感器（它不影响小球运动，在图中未画出）。将一个小球从左侧直轨道上的某处由静止释放，并测得释放处距离圆轨道最低点的竖直高度为h，记录小球通过最高点时对轨道（压力传感器）的压力大小为F。此后不断改变小球在左侧直轨道上释放位置，重复实验，经多次测量，得到了多组h和F，把这些数据标在F-h图中，并用一条直线拟合，结果如图所示。
为了方便研究，研学小组把小球简化为质点，并忽略空气及轨道对小球运动的阻力，取重力加速度g=10m/s2。请根据该研学小组的简化模型和如图所示的F-h图
（1）当释放高度h=0.20m时，小球到达圆轨道最低点时的速度大小v；
（2）圆轨道的半径R和小球的质量m；
（3）若两段倾斜直轨道都足够长，为使小球在运动过程中始终不脱离圆轨道，释放高度h应满足什么条件。
【答案】（1）
（2）R=0.12m ，m=0.02kg（3）h≤0.12m或者h≥0.3m
【解析】
（1）设小球质量为m，对于从释放到轨道最低点的过程，根据动能定理，有
解得：
（2）设小球到达A点速度为vA，根据动能定理
在A点，设轨道对小球的压力为N，根据牛顿第二定律：
根据牛顿第三定律
N=F
联立上述三式可得：
对比F-h图像，根据斜率和截距关系，可得：
R=0.12m
m=0.02kg
（3）假设h=h1时，小球恰好到达最高点A，此时F=0
由F-h图像可得：
h1=0.3m
假设h=h2时，小球恰好到达圆轨道圆心的右侧等高点，此过程根据动能定理：
解得：
h2=R=0.12m
综上，为使小球在运动过程中始终不脱离圆轨道，释放高度h应满足：
h≤0.12m或者h≥0.3m
