题目内容
5.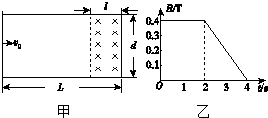 如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”形导轨,在“U”形导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2).
如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”形导轨,在“U”形导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2).(1)通过计算分析4s内导体棒的运动情况;
(2)计算4s内回路中电流的大小,并判断电流方向;
(3)计算4s内回路产生的焦耳热.
分析 导体棒在没有磁场区域,由于摩擦阻力做匀减速运动,由牛顿第二定律求出加速度,然后确定4s棒的运动情况.回路中前2S内没有磁通量变化,后2S内磁通量均匀变小,产生的电动势不变,则电流恒定,故由焦耳定律可求出产生的热量.
解答 解:(1)导体棒先在无磁场区域做匀减速运动,有
-μmg=ma
vt=v0+at
x=v0t+$\frac{1}{2}$at2
导体棒速度减为零时,vt=0
代入数据解得:t=1 s,x=0.5 m,因x<L-l,故导体棒没有进入磁场区域.
导体棒在1 s末已停止运动,以后一直保持静止,离左端位置仍为x=0.5 m
(2)前2 s磁通量不变,回路电动势和电流分别为
E=0,I=0
后2 s回路产生的电动势为
E=$\frac{△Φ}{△t}$=ld$\frac{△B}{△t}$=0.1 V
回路的总长度为5 m,因此回路的总电阻为
R=5λ=0.5Ω
电流为I=$\frac{E}{R}$=0.2 A
根据楞次定律,在回路中的电流方向是顺时针方向.
(3)前2 s电流为零,后2 s有恒定电流,回路产生的焦耳热为
Q=I2Rt=0.04 J.
答:(1)导体棒在1 s末已停止运动,以后一直保持静止,离左端位置仍为x=0.5 m;
(2)4s内回路中电流的大小0.2 A,电流方向顺时针方向;
(3)则4s内回路产生的焦耳热0.04 J.
点评 法拉第电磁感应定律求感应电动势,由闭合电路殴姆定律可列出电动势与电流的关系.楞次定律是判定感应电流方向,焦耳定律可求出电阻的发热量.

练习册系列答案
相关题目
16. 图甲是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并分别与高频电源两极相连.带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,若忽略带电粒子在电场中的加速时间,则下列说法正确的是( )
图甲是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并分别与高频电源两极相连.带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,若忽略带电粒子在电场中的加速时间,则下列说法正确的是( )
 图甲是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并分别与高频电源两极相连.带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,若忽略带电粒子在电场中的加速时间,则下列说法正确的是( )
图甲是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并分别与高频电源两极相连.带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,若忽略带电粒子在电场中的加速时间,则下列说法正确的是( )| A. | (t2-tl)>(t3-t2)>…>(tn-tn-l) | |
| B. | 高频电源的变化周期应该等于tn-tn-l | |
| C. | 要使粒子获得的最大动能增大,可以增大D形盒的半径 | |
| D. | 要使粒子获得的最大动能增大,可以增大加速电压 |
13. 如图,是一条与Ox轴重合的电场线上各点的电势φ随x变化的图线.若在x0点由静止释放一个点电荷,取x0处的电势为零,则在电荷运动的过程中,下列说法中正确的是( )
如图,是一条与Ox轴重合的电场线上各点的电势φ随x变化的图线.若在x0点由静止释放一个点电荷,取x0处的电势为零,则在电荷运动的过程中,下列说法中正确的是( )
 如图,是一条与Ox轴重合的电场线上各点的电势φ随x变化的图线.若在x0点由静止释放一个点电荷,取x0处的电势为零,则在电荷运动的过程中,下列说法中正确的是( )
如图,是一条与Ox轴重合的电场线上各点的电势φ随x变化的图线.若在x0点由静止释放一个点电荷,取x0处的电势为零,则在电荷运动的过程中,下列说法中正确的是( )| A. | 电荷一定沿x轴正方向运动 | B. | 电场的场强在逐渐减弱 | ||
| C. | 电荷的电势能可能为正 | D. | 电场力一定做正功 |
20.小船在静水中的速度是4m/s,水流速度为3m/s,河的宽度为200m.则( )
| A. | 小船不可能到达正对岸 | |
| B. | 小船渡河到达对岸通过的位移最短为250m | |
| C. | 小船渡河到达对岸的时间不会少于50s | |
| D. | 小船在水中的运动轨迹是一条曲线 |
14.北京时间2012年3月31日,中国在西昌卫星发射中心用“长征三号乙”运载火箭,将法国制造的“亚太7号”通信卫星成功送入近地点209km、远地点50 419km的预定转移轨道,卫星在此轨道上运行一段时间后再经变轨成为一颗地球同步卫星,同步卫星轨道离地面高度为35 860km.下列说法正确的是( )
| A. | 卫星在转移轨道运行的周期大于在同步轨道上运行的周期 | |
| B. | 星在转移轨道运动时,经过近地点时的速率大于它在远地点的速率 | |
| C. | 卫星在同步轨道运动时,飞船内的航天员处于超重状态 | |
| D. | 卫星在同步轨道运动时的向心加速度小于静止于赤道上物体的向心加速度 |
 用如图所示的电路测量一节蓄电池的电动势和内阻,蓄电池的内阻非常小,为防止调节滑动变阻器电阻过小时由于电流过大而损坏器材,电路中用了一个保护电阻R0,除蓄电池、开关、导线外,可供选择使用的实验器材还有:
用如图所示的电路测量一节蓄电池的电动势和内阻,蓄电池的内阻非常小,为防止调节滑动变阻器电阻过小时由于电流过大而损坏器材,电路中用了一个保护电阻R0,除蓄电池、开关、导线外,可供选择使用的实验器材还有: 总质量为M的火箭被飞机释放时的速度为v0,方向水平.释放后火箭立即向后以相对于地面的速率u喷出质量为m的燃气,火箭相对于地面的速度变为多大?
总质量为M的火箭被飞机释放时的速度为v0,方向水平.释放后火箭立即向后以相对于地面的速率u喷出质量为m的燃气,火箭相对于地面的速度变为多大? 一多用电表的欧姆挡有4挡,分别为×1Ω,×10Ω,×100Ω,×1000Ω,现用它来测一未知电阻值.当用×100Ω挡测量时,发现指针的偏转角度很小. 为了使测量结果更准确,必须先换用×1000Ω接着进行欧姆调零,然后再测量并读数.
一多用电表的欧姆挡有4挡,分别为×1Ω,×10Ω,×100Ω,×1000Ω,现用它来测一未知电阻值.当用×100Ω挡测量时,发现指针的偏转角度很小. 为了使测量结果更准确,必须先换用×1000Ω接着进行欧姆调零,然后再测量并读数.