题目内容
10.放射性原子核${\;}_{92}^{238}U$先后发生α衰变和β衰变后,变为原子核${\;}_{91}^{234}Pa$.已知${\;}_{92}^{238}U$质量为m1=238.0290u;${\;}_{91}^{234}Pa$质量为m2=234.0239u,α粒子的质量为mα=4.0026u,电子的质量为me=0.0005u.(原子质量单位1u相当于931MeV的能量).则:①放射性衰变方程为:${\;}_{92}^{238}U→{\;}_{91}^{234}Pa+{\;}_2^4He+{\;}_{-1}^0e$;
②原子核${\;}_{92}^{238}U$衰变为${\;}_{91}^{234}Pa$的过程中释放能量为1.86MeV(保留三位有效数字).
③在第②问中,若原来${\;}_{92}^{238}U$静止,衰变后放出的α粒子速度为Vα=3×107m/s,不计电子和衰变过程中释放光子的动量,则${\;}_{91}^{234}Pa$的速度大小约为5.1×105m/s(保留两位有效数字)?(请写出必要的解答过程)
分析 (1)根据质量数和电荷数守恒可正确书写该衰变方程.
(2)衰变过程满足质能方程,根据这个方程列方程即可求解.
(3)根据动量守恒定律,即可求解.
解答 解:(1)根据质量数和电荷数守恒,衰变方程为:${\;}_{92}^{238}$U→${\;}_{91}^{234}Pa$+${\;}_{2}^{4}He$+${\;}_{-1}^{0}e$.
(2)上述衰变过程的质量亏损为:△m=mu-mPa-mα -me
放出的能量为:△E=c2•△m
代入题给数据得:△E=23 8.0290-234.0239-4.0026-0.0005u=0.002×931=1.86MeV.
(3)核衰变过程系统动量守恒,以α粒子动量方向为正方向,由动量守恒定律得:
0=mαvα+m2v2,
解得:v2=$\frac{{m}_{α}{v}_{α}}{{m}_{2}}$=$\frac{4.0026×3×1{0}^{7}}{234.0239}$=5.1×105m/s;
故答案为:①${\;}_{92}^{238}U→{\;}_{91}^{234}Pa+{\;}_2^4He+{\;}_{-1}^0e$;②1.86;③5.1×105m/s
点评 本题考查衰变与爱因斯坦质能方程,根据质量数守恒与核电荷数守恒即可正确写出核反应方程,应用质能方程与动量守恒定律即可正确解题.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 布朗运动就是悬浮固体小颗粒内分子的无规则运动 | |
| B. | 卢瑟福α粒子散射实验说明原子核内部具有复杂的结构 | |
| C. | 内燃机可以把内能全部转化为机械能 | |
| D. | 热量不可能自发地从低温物体传到高温物体 |
19.如图甲所示,理想变压器原、副线圈的匝数比为5:1,原线圈接交流电源和交流电压,副线圈接有“220V,440W”的热水器、“220V,220W”的抽油烟机.如果副线圈电压按图乙所示规律变化,则下列说法正确的是( )


| A. | 副线圈两端电压的瞬时值为u=440$\sqrt{2}$sin(100πt)V | |
| B. | 变流电压表的示数为1100$\sqrt{2}$V | |
| C. | 1min内变压器输出的电能为3.96×104J | |
| D. | 热水器的发热功率是抽油烟机发热功率的2倍 |
20.下列说法中正确的是( )
| A. | 只要每分钟的位移相等,物体一定做匀速直线运动 | |
| B. | 研究乒乓球旋转时,可以把它看成质点 | |
| C. | 物体沿一直线向某方向运动,那么通过的路程就是位移 | |
| D. | 排球着地时的瞬时速度是20m/s |
 如图所示为某学校一套校内备用供电系统,由一台内阻r=19Ω的发电机向全校22个教室(每个教室有“220V 40W”的白炽灯6盏)供电,理想降压变压器的原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{19}{11}$,不计导线电阻,当灯都正常工作时:
如图所示为某学校一套校内备用供电系统,由一台内阻r=19Ω的发电机向全校22个教室(每个教室有“220V 40W”的白炽灯6盏)供电,理想降压变压器的原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{19}{11}$,不计导线电阻,当灯都正常工作时:
 如图所示,间距为L的平行光滑金属导轨与水平面的夹角为θ,导轨电阻不计.导体棒ab、cd垂直导轨放置,棒长均为L,电阻均为R,且与导轨电接触良好.ab棒处于垂直导轨平面向上、磁感应强度B1随时间均匀增加的匀强磁场中.Cd棒质量为m,处于垂直导轨平面向上、磁感应强度恒为B2的匀强磁场中,恰好保持静止.ab棒在外力作用下也保持静止,重力加速度为g.
如图所示,间距为L的平行光滑金属导轨与水平面的夹角为θ,导轨电阻不计.导体棒ab、cd垂直导轨放置,棒长均为L,电阻均为R,且与导轨电接触良好.ab棒处于垂直导轨平面向上、磁感应强度B1随时间均匀增加的匀强磁场中.Cd棒质量为m,处于垂直导轨平面向上、磁感应强度恒为B2的匀强磁场中,恰好保持静止.ab棒在外力作用下也保持静止,重力加速度为g.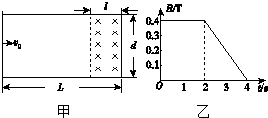 如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”形导轨,在“U”形导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2).
如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”形导轨,在“U”形导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2).