题目内容
20.小船在静水中的速度是4m/s,水流速度为3m/s,河的宽度为200m.则( )| A. | 小船不可能到达正对岸 | |
| B. | 小船渡河到达对岸通过的位移最短为250m | |
| C. | 小船渡河到达对岸的时间不会少于50s | |
| D. | 小船在水中的运动轨迹是一条曲线 |
分析 A、通过比较船在静水中的速度和河水速度的大小,可判断出船是否能垂直渡河,继而可知选项A的正误.
B、结合A选项的解答,可知船渡河的最短位移为河的宽度,
C、船在静水中的速度垂直于河岸时,用时最小,可以计算出最小时间玛继而得知该选项的正误.
D、分析合加速度的情况,可判断小船的运动情况,继而得知选项D的正误.
解答 解:AB、因为船在静水中的速度大于河水的流速,由平行四边形法则求合速度可以垂直河岸,小船能垂直河岸正达对岸.同时得知小船渡河到达对岸通过的位移最短为200m,所以选项AB错误.
C、当船的静水中的速度垂直河岸时渡河时间最短:tmin=$\frac{d}{{v}_{船}}$=$\frac{200}{4}$=50s,小船渡河到达对岸的时间不会少于50s,故C正确.
D、小船在水中参与的两个运动都是匀速直线运动,合加速度为零,所以小船做匀速直线运动,运动轨迹是直线,选项D错误.
故选:C
点评 解决本题的关键知道分运动和合运动具有等时性,各分运动具有独立性.要明确水流速度的变化对对河路程的影响.
该题通过渡河的模型考察了运动的合成与分解,关于渡河问题,应注意几种渡河方式:
一是垂直渡河,此时渡河位移最短,但是所用时间不是最短的,此种情况要求船的合速度与河岸垂直,
二是船头始终指向对岸的渡河,此种情况下渡河时间最短,但是渡河位移不是最短,最短渡河时间不受水速的影响;
关于渡河问题,还要会判断能否垂直渡河,其条件是船在静水中的速度大小要大于河水流动的速度大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 在如图所示的电路中,L是电感线圈,R1、R2是电阻,两个灵敏电流表G1和G2的零点都在刻度盘中央,当电流从“+”接线柱流入时,指针向右摆,电流从“-”接线柱流入时,指针向左摆,在电路接通后再断开的瞬间,下列说法符合实际的情况是( )
在如图所示的电路中,L是电感线圈,R1、R2是电阻,两个灵敏电流表G1和G2的零点都在刻度盘中央,当电流从“+”接线柱流入时,指针向右摆,电流从“-”接线柱流入时,指针向左摆,在电路接通后再断开的瞬间,下列说法符合实际的情况是( )
 在如图所示的电路中,L是电感线圈,R1、R2是电阻,两个灵敏电流表G1和G2的零点都在刻度盘中央,当电流从“+”接线柱流入时,指针向右摆,电流从“-”接线柱流入时,指针向左摆,在电路接通后再断开的瞬间,下列说法符合实际的情况是( )
在如图所示的电路中,L是电感线圈,R1、R2是电阻,两个灵敏电流表G1和G2的零点都在刻度盘中央,当电流从“+”接线柱流入时,指针向右摆,电流从“-”接线柱流入时,指针向左摆,在电路接通后再断开的瞬间,下列说法符合实际的情况是( )| A. | G1、G2表的指针都向右摆 | |
| B. | G1、G2表的指针都向左摆 | |
| C. | G1表的指针向右摆,G2表的指针向左摆 | |
| D. | G1表的指针向左摆,G2表的指针向右摆 |
11.下面是一些有关高中物理实验的描述,其中正确的是 ( )
| A. | 在“研究匀变速直线运动”实验中,不需要平衡摩擦力 | |
| B. | 在“验证机械能守恒定律”的实验中,必须用天平测物体的质量 | |
| C. | 在“探究力的平行四边形定则”的实验中,在同一次实验中橡皮条拉长的结点O位置可以不同 | |
| D. | 在用橡皮筋“探究功与速度变化的关系”的实验中不需要直接求出合外力做的功 | |
| E. | 在用欧姆表“×10”挡测量电阻时发现指针偏转角太小,应该换“×1”挡进行测量 |
8. 如图所示,理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端A、A1、A2、A3 为理想的交流电流表,R为三个完全相同的电阻,L为电感,C为电容,当输入端接通电源后,电流表A 读数为I.下列判断正确的是( )
如图所示,理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端A、A1、A2、A3 为理想的交流电流表,R为三个完全相同的电阻,L为电感,C为电容,当输入端接通电源后,电流表A 读数为I.下列判断正确的是( )
 如图所示,理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端A、A1、A2、A3 为理想的交流电流表,R为三个完全相同的电阻,L为电感,C为电容,当输入端接通电源后,电流表A 读数为I.下列判断正确的是( )
如图所示,理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端A、A1、A2、A3 为理想的交流电流表,R为三个完全相同的电阻,L为电感,C为电容,当输入端接通电源后,电流表A 读数为I.下列判断正确的是( )| A. | 副线圈两端的电压为nU | |
| B. | 通过副线圈的最大电流I | |
| C. | 电流表A1 的读数I1 大于电流表A2 的读数I2 | |
| D. | 电流表A3 的读数I3=0 |
15.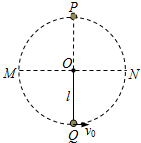 “水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,忽略空气阻力,则( )
“水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,忽略空气阻力,则( )
 “水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,忽略空气阻力,则( )
“水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,忽略空气阻力,则( )| A. | 小球运动到最低点Q时,处于超重状态 | |
| B. | 小球初速度v0越大,则在P、Q两点绳对小球的拉力差越大 | |
| C. | 当v0>$\sqrt{6gl}$,小球一定能通过最高点P | |
| D. | 当v0<$\sqrt{gl}$,细绳始终处于绷紧状态 |
9. 如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦).当用水平拉力F拉动物体B沿水平方向向右做匀速直线运动,则( )
如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦).当用水平拉力F拉动物体B沿水平方向向右做匀速直线运动,则( )
 如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦).当用水平拉力F拉动物体B沿水平方向向右做匀速直线运动,则( )
如图所示,物体A和B的质量均为m,且分别用轻绳连接跨过定滑轮(不计绳子与滑轮、滑轮与轴之间的摩擦).当用水平拉力F拉动物体B沿水平方向向右做匀速直线运动,则( )| A. | 物体A也做匀速直线运动 | |
| B. | 物体A作匀加速直线运动 | |
| C. | 物体A的速度增大,但一直小于物体B的速度 | |
| D. | 物体A的速度增大,可能最终等于或者大于物体B的速度 |
10.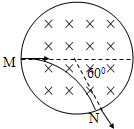 在半径为R的圆形区域内有磁感应强度为B的匀强磁场,一个电子(电荷量为e,质量为m)从M点沿半径方向以速度v0射入,从N点射出时的速度方向偏转了60°,如图则电子从M到N运行的时间是( )
在半径为R的圆形区域内有磁感应强度为B的匀强磁场,一个电子(电荷量为e,质量为m)从M点沿半径方向以速度v0射入,从N点射出时的速度方向偏转了60°,如图则电子从M到N运行的时间是( )
 在半径为R的圆形区域内有磁感应强度为B的匀强磁场,一个电子(电荷量为e,质量为m)从M点沿半径方向以速度v0射入,从N点射出时的速度方向偏转了60°,如图则电子从M到N运行的时间是( )
在半径为R的圆形区域内有磁感应强度为B的匀强磁场,一个电子(电荷量为e,质量为m)从M点沿半径方向以速度v0射入,从N点射出时的速度方向偏转了60°,如图则电子从M到N运行的时间是( )| A. | $\frac{πm}{3eB}$ | B. | $\frac{πm}{6eB}$ | C. | 、$\frac{πR}{{3{v_0}}}$ | D. | $\frac{{\sqrt{3}πR}}{{3{v_0}}}$ |
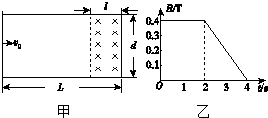 如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”形导轨,在“U”形导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2).
如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”形导轨,在“U”形导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2).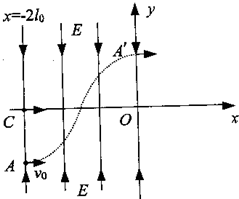 如图所示的直角坐标系中,在直线x=-2l0的y轴区域内存在两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场的方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电荷量为+q,质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用.
如图所示的直角坐标系中,在直线x=-2l0的y轴区域内存在两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场的方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电荷量为+q,质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用.