题目内容
16. 图甲是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并分别与高频电源两极相连.带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,若忽略带电粒子在电场中的加速时间,则下列说法正确的是( )
图甲是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并分别与高频电源两极相连.带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示,若忽略带电粒子在电场中的加速时间,则下列说法正确的是( )| A. | (t2-tl)>(t3-t2)>…>(tn-tn-l) | |
| B. | 高频电源的变化周期应该等于tn-tn-l | |
| C. | 要使粒子获得的最大动能增大,可以增大D形盒的半径 | |
| D. | 要使粒子获得的最大动能增大,可以增大加速电压 |
分析 交流电源的周期必须和粒子在磁场中运动的周期一致,由公式T=$\frac{2πm}{qB}$和r=$\frac{mv}{qB}$判断;当粒子从D形盒中出来时,速度最大,此时运动的半径等于D形盒的半径.
解答 解:A、洛伦兹力提供向心力,有qvB=m$\frac{{v}^{2}}{r}$,解得r=$\frac{mv}{qB}$,故周期T=$\frac{2πr}{v}$=$\frac{2πm}{qB}$,
与速度无关,故t4-t3=t3-t2=t2-t1=$\frac{T}{2}$,故A错误;
B、交流电源的周期必须和粒子在磁场中运动的周期一致,故高频电源的变化周期应该等于2(tn-tn-1),故B错误;
C、当粒子从D形盒中出来时,速度最大,此时运动的半径等于D形盒的半径;
由qvB=m$\frac{{v}^{2}}{R}$得,v=$\frac{qRB}{m}$,则最大动能EK=$\frac{1}{2}$mv2=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$,知最大动能与加速器的半径、磁感线强度以及电荷的电量和质量有关,与加速电压等其他因素无关,故C正确;
D、当粒子从D形盒中出来时,速度最大,此时运动的半径等于D形盒的半径;
由qvB=m$\frac{{v}^{2}}{R}$得,v=$\frac{qRB}{m}$,则最大动能EK=$\frac{1}{2}$mv2=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$,知最大动能与加速器的半径、磁感线强度以及电荷的电量和质量有关,与加速电压无关,故D错误;
故选:C.
点评 解决本题的关键知道回旋加速器是利用电场加速、磁场偏转来加速粒子,但是最终粒子的动能与电场的大小无关.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
10.下列关于惯性的说法正确的是( )
| A. | 物体只有在静止或做匀速直线运动时才有惯性 | |
| B. | 乘坐汽车时系好安全带可减小乘客的惯性 | |
| C. | 速度大的汽车不容易停下来,说明汽车运动时的惯性比静止时的惯性大 | |
| D. | “月兔”探测器在地球上和月球上的惯性一样大 |
4.质量m的滑块,以初速度V0沿光滑斜面向上滑行,当滑块从斜面底端滑到高度为h的地方时,滑块的机械能是( )
| A. | $\frac{1}{2}$m V02+mgh | B. | mgh | C. | $\frac{1}{2}$mV02-mgh | D. | $\frac{1}{2}$mV02 |
11.下面是一些有关高中物理实验的描述,其中正确的是 ( )
| A. | 在“研究匀变速直线运动”实验中,不需要平衡摩擦力 | |
| B. | 在“验证机械能守恒定律”的实验中,必须用天平测物体的质量 | |
| C. | 在“探究力的平行四边形定则”的实验中,在同一次实验中橡皮条拉长的结点O位置可以不同 | |
| D. | 在用橡皮筋“探究功与速度变化的关系”的实验中不需要直接求出合外力做的功 | |
| E. | 在用欧姆表“×10”挡测量电阻时发现指针偏转角太小,应该换“×1”挡进行测量 |
8. 如图所示,理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端A、A1、A2、A3 为理想的交流电流表,R为三个完全相同的电阻,L为电感,C为电容,当输入端接通电源后,电流表A 读数为I.下列判断正确的是( )
如图所示,理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端A、A1、A2、A3 为理想的交流电流表,R为三个完全相同的电阻,L为电感,C为电容,当输入端接通电源后,电流表A 读数为I.下列判断正确的是( )
 如图所示,理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端A、A1、A2、A3 为理想的交流电流表,R为三个完全相同的电阻,L为电感,C为电容,当输入端接通电源后,电流表A 读数为I.下列判断正确的是( )
如图所示,理想变压器,原副线圈的匝数比为n.原线圈接正弦交流电压U,输出端A、A1、A2、A3 为理想的交流电流表,R为三个完全相同的电阻,L为电感,C为电容,当输入端接通电源后,电流表A 读数为I.下列判断正确的是( )| A. | 副线圈两端的电压为nU | |
| B. | 通过副线圈的最大电流I | |
| C. | 电流表A1 的读数I1 大于电流表A2 的读数I2 | |
| D. | 电流表A3 的读数I3=0 |
 气垫导轨是利用气泵使带孔的导轨与滑块之间形成“气垫”,使滑块悬浮在导轨上,滑块在导轨上运动时可不计摩擦,现用带竖直挡板C、D的气垫导轨和滑块A、B验证动量守恒定律,实验装置如图所示,有以下实验步骤:
气垫导轨是利用气泵使带孔的导轨与滑块之间形成“气垫”,使滑块悬浮在导轨上,滑块在导轨上运动时可不计摩擦,现用带竖直挡板C、D的气垫导轨和滑块A、B验证动量守恒定律,实验装置如图所示,有以下实验步骤:
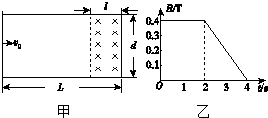 如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”形导轨,在“U”形导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2).
如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”形导轨,在“U”形导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2). 在“探究平抛运动的规律”的实验中,分成两步进行:
在“探究平抛运动的规律”的实验中,分成两步进行: