题目内容
12.某河水流速度为5m/s,一小船在静水中的速度大小是4m/s,要渡过此河,船头垂直河岸行驶,已知河宽为120m,试问:(1)小船能否渡河直达正对岸?
(2)船需多少时间才能到达对岸?
(3)此船登上对岸的地点离出发点的距离是多少?
(4)若船行至正中间时,河水流速增大到8m/s,则船渡河需要多少时间?登岸地点如何变化?
(5)此船过河的最短位移是多大?
分析 (1)通过判断合速度能否与河岸垂直,判断船能否垂直到对岸;
(2)将船的运动分解为沿河岸方向和垂直于河岸方向,根据垂直于河岸方向上的速度求出渡河的时间.
(3)根据船头垂直河岸行驶的时间,从而确定沿着水流的位移,依据运动的合成,即可求解;
(4)因船头垂直河岸行驶,水流速度不会影响渡河时间,但导致水流方向的位移变化,从而即可求解;
(5)运用作图法,根据三角形定则分析什么条件下船的合速度与河岸夹角最大,则船登陆的地点离船出发点的最小距离,再由几何知识求解最小距离.
解答 解:(1)船对静水的速度小于水速,则船的合速度不可能垂直河岸时,因此船不能垂直渡过河.
(2)因船头垂直河岸行驶,则渡河时间为:t=$\frac{d}{{v}_{c}}$=$\frac{120}{4}$s=30s.
(3)当船垂直河岸过河后,沿着水流方向的位移为:s=vst=5×30=150m;
那么登上对岸的地点离出发的距离为:x=$\sqrt{{s}^{2}+{d}^{2}}$=$\sqrt{15{0}^{2}+12{0}^{2}}$=192m;
(4)河水流速增大到8m/s,不影响船渡河需要时间,仍为30s,因水流速度的增大,则登岸地点继续偏向下游;
(5) 船实际是按合速度方向运动,由于v1、v2的大小一定,根据作图法,由三角形定则分析可知,当船相对于水的速度v1与合速度垂直时,合速度与河岸的夹角最大,船登陆的地点离船出发点的最小距离.设船登陆的地点离船出发点的最小距离为S.根据几何知识得$\frac{d}{s}$=$\frac{{v}_{1}}{{v}_{2}}$ 代入解得 S=150m.
船实际是按合速度方向运动,由于v1、v2的大小一定,根据作图法,由三角形定则分析可知,当船相对于水的速度v1与合速度垂直时,合速度与河岸的夹角最大,船登陆的地点离船出发点的最小距离.设船登陆的地点离船出发点的最小距离为S.根据几何知识得$\frac{d}{s}$=$\frac{{v}_{1}}{{v}_{2}}$ 代入解得 S=150m.
答:(1)小船不能渡河直达正对岸;
(2)船需30s时间才能到达对岸;
(3)此船登上对岸的地点离出发的距离是192m;
(4)若船行至河正中间时,河水流速增大到8m/s,则船渡河需要30s时间,登岸地点继续偏向下游;
(5)此船过河的最短位移是150m.
点评 考查是小船渡河问题,解决本题的关键知道合运动与合运动具有等时性,各分运动具有独立性,互不干扰.同时运用运动的合成与分解作出速度分解或合成图,分析最短时间或最短位移渡河的条件.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | 做曲线运动的物体在某段时间内的平均速度,一定和物体在这段时间内各个时刻的瞬时速度的平均值大小相等 | |
| B. | 某时刻物体速度为零,其加速度不可能很大 | |
| C. | 研究跳水运动员下落时间时,运动员不可视为质点 | |
| D. | 参考系可以是变速运动的物体 |
| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 无法确定 |
 如图所示,一圆柱形导热良好的气瓶水平放置,瓶内有用导热良好的活塞分开的A、B两部分,分别装有理想气体.活塞与瓶内壁气密性好,并可在瓶内自由移动,不计摩擦,开始时,A、B两部分气体的体积之比为2:1,压强均为p,大气温度为T,K为阀门.
如图所示,一圆柱形导热良好的气瓶水平放置,瓶内有用导热良好的活塞分开的A、B两部分,分别装有理想气体.活塞与瓶内壁气密性好,并可在瓶内自由移动,不计摩擦,开始时,A、B两部分气体的体积之比为2:1,压强均为p,大气温度为T,K为阀门.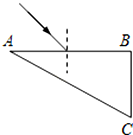 直角三角形玻璃砖ABC,其中∠A=30°,平放于水平桌面上,如图为其俯视图.一束单色光以45°的入射角水平射入其AB面,在AB面折射后又在AC面处发生一次反射,最后垂直于BC面穿出玻璃砖.
直角三角形玻璃砖ABC,其中∠A=30°,平放于水平桌面上,如图为其俯视图.一束单色光以45°的入射角水平射入其AB面,在AB面折射后又在AC面处发生一次反射,最后垂直于BC面穿出玻璃砖.