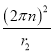题目内容
【题目】如图所示,在直角坐标系Oxy中,虚线ACD是以坐标原点O为圆心、以AD=0.2m为直径的半圆,AD在x轴上,在y≥0的空间内有垂直纸面向外的匀强磁场,磁感应强度大小为B=0.667T。在半圆弧ACD上某处有一质子源S,当S在ACD上的不同位置时,总是沿+y方向发射速度为v=1.6×106m/s的质子,质子的质量m=6.67×10-27kg,电荷量g=1.6×10-19C,不计质子重力。设圆心角∠AOS=θ,下列说法正确的是
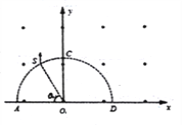
A. 当θ≤90°时,质子源发射的质子在磁场中运动时都经过D点
B. 当θ=120°时,质子源发射的质子在磁场中运动的时间为![]() ×10-6s
×10-6s
C. 质子源发射的质子在磁场中运动的最长时间为![]() ×10-6s
×10-6s
D. 质子源发射的质子在磁场中运动最短时间为![]() ×10-6s
×10-6s
【答案】ACD
【解析】A、根据半径公式![]() ,即质子轨迹半径与圆弧半径相同,
,即质子轨迹半径与圆弧半径相同,
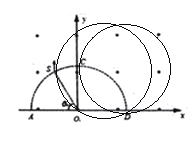
根据几何关系可知,质子恰好过D点,故A正确;
B、当θ=120°时,画出质子轨迹如图
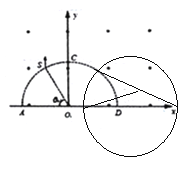
由几何关系可知圆心角为2400,质子源发射的质子在磁场中运动的时间为![]() ,故B错误;
,故B错误;
CD、由于发射速度一定,质子源发射的质子在磁场中运动的最长时间,则对应的弧长最长,由几何关系可得最大圆心角为2700,质子源发射的质子在磁场中运动的最长时间![]() ,质子源发射的质子在磁场中运动的最短时间,则对应的弧长最短,由几何关系可得最大圆心角为1800,质子源发射的质子在磁场中运动最短时间为
,质子源发射的质子在磁场中运动的最短时间,则对应的弧长最短,由几何关系可得最大圆心角为1800,质子源发射的质子在磁场中运动最短时间为![]() ,故CD正确。
,故CD正确。
故选ACD。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目