题目内容
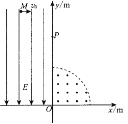
【题目】如图所示,xOy坐标系位于竖直平面内,在其第一象限以O点为园心的![]() 圆形区域内存在一个有界匀强磁场,磁场的磁感应强度大小为B,方向垂直于坐标平面向外。在第二象限内存在沿y轴负方向的匀强电场,电场强度E=
圆形区域内存在一个有界匀强磁场,磁场的磁感应强度大小为B,方向垂直于坐标平面向外。在第二象限内存在沿y轴负方向的匀强电场,电场强度E=![]() 。质量为m、带电荷量为+q的粒子从电场中与y轴距离为L的M点以大小为v0的初速度沿x轴正方向射出,穿过y轴上的P点,从磁场边界上的N点(图中未画出)射人磁场,最后粒子从O点沿x轴负方向射出磁场,不计粒子重力。求:
。质量为m、带电荷量为+q的粒子从电场中与y轴距离为L的M点以大小为v0的初速度沿x轴正方向射出,穿过y轴上的P点,从磁场边界上的N点(图中未画出)射人磁场,最后粒子从O点沿x轴负方向射出磁场,不计粒子重力。求:
(1)粒子经过P点时的速度。
(2)粒子在磁场中运动轨迹的半径与磁场半径的比值和粒子在磁场中运动的时间。
【答案】(1)![]() ,与y轴负方向成30度斜角右下方(2)
,与y轴负方向成30度斜角右下方(2)![]()
【解析】
(1)粒子在电场中做类平抛运动,如图甲所示

设粒子在电场中的加速度为![]() ,在P点沿电场方向的速度为
,在P点沿电场方向的速度为![]() ,在P点的速度为v,其与y轴负方向的夹角为θ,粒子从M点运动到P点的时间为
,在P点的速度为v,其与y轴负方向的夹角为θ,粒子从M点运动到P点的时间为![]() ,则有
,则有
![]()
![]()
![]()
![]()
联立解得![]()
![]() ,即
,即![]()
故粒子经过P点时的速度方向与y轴负方向成30°角斜向右下方;
(2)粒子从P点射出后的运动轨迹如图乙所示

由几何关系可知,粒子在磁场中转过的圆心角![]() ,又
,又![]() ,则
,则![]()
设粒子在磁场中运动轨迹的半径为r,磁场的半径为R,由几何关系得:![]()
解得:![]()
粒子在磁场中转过的弧长![]()
运动时间![]()
在磁场中有![]()
联立解得:![]()

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目