题目内容
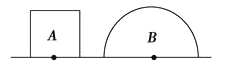
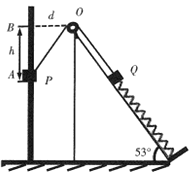
【题目】一劲度系数为k=100N/m的轻弹簧下端固定于倾角为θ=53°的光滑斜面底端，上端连接物块Q。一轻绳跨过定滑轮O，一端与物块Q连接，另一端与套在光滑竖直杆的物块P连接，定滑轮到竖直杆的距离为d=0.3m。初始时在外力作用下，物块P在A点静止不动，轻绳与斜面平行，绳子张力大小为50N。已知物块P质量为m1=0.8kg，物块Q质量为m2=5kg，不计滑轮大小及摩擦，取g=10m/s2。现将物块P静止释放，求：
(1)物块P位于A时，弹簧的伸长量x1；
(2)物块P上升h=0.4m至与滑轮O等高的B点时的速度大小；
(3)物块P上升至B点过程中，轻绳拉力对其所做的功。
【答案】（1）0.1m （2）
（3）8J
【解析】
（1）根据题设条件和平衡条件、胡克定律，列方程求出弹簧的伸长量；
（2）由于本题的特殊性，P处于A位置时与P上升到与滑轮等高位置，弹簧的伸长量与压缩量恰相等，而此时由速度的合成和分解可知物块Q的速度为零，所以由机械能守恒律可求物块P的速度；
（3）当Q上升到与滑轮等高时，由系统的机械能守恒和两个物体速度关系求圆环Q的速度大小。通过绳子拉力对Q物体的做功情况，判断物块Q机械能的变化，从而得出何时机械能最大。
（1）物体P位于A点，假设弹簧伸长量为
，则：
，解得：
（2）经分析，此时OB垂直竖直杆，OB=0.3m，此时物块Q速度为0，下降距离为：
，即弹簧压缩
，弹性势能不变。
对物体PQ及弹簧，从A到B根据能量守恒有：
代入可得：
对物块P：
代入数据得：
练习册系列答案
相关题目
