题目内容
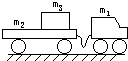 在光滑水平面上,有一质量m1=20kg的小车,通过一根几乎不可伸长的轻绳与另一个质量为m2=25kg的拖车相连接.一质量m3=15kg的物体放在拖车的平板上.物体与平板间的动摩擦因数为μ=0.20.开始时,拖车静止,绳未拉紧,如图所示,小车以v0=3m/s的速度向前运动.求:
在光滑水平面上,有一质量m1=20kg的小车,通过一根几乎不可伸长的轻绳与另一个质量为m2=25kg的拖车相连接.一质量m3=15kg的物体放在拖车的平板上.物体与平板间的动摩擦因数为μ=0.20.开始时,拖车静止,绳未拉紧,如图所示,小车以v0=3m/s的速度向前运动.求:(1)当m1、m2、m3以同一速度前进时,速度的大小.
(2)物体在拖车平板上移动的距离.(g取10m/s2)
分析:(1)将小车、拖车和物体三个物体看成一系统,在水平方向上动量守恒,根据动量守恒定律求出三者一起运动的速度大小.
(2)轻绳从伸直到拉紧的时间极短,在此过程中,小车与拖车在水平方向上动量守恒,根据动量守恒求出小车和拖车的共同速度,然后物体在拖车上发生相对滑动,根据动能定理求出拖车和小车整体与物体的位移,从而求出它们的相对位移.
(2)轻绳从伸直到拉紧的时间极短,在此过程中,小车与拖车在水平方向上动量守恒,根据动量守恒求出小车和拖车的共同速度,然后物体在拖车上发生相对滑动,根据动能定理求出拖车和小车整体与物体的位移,从而求出它们的相对位移.
解答:解:(1)由小车、拖车和物体三者水平方向动量守恒:m1v0=(m1+m2+m3)u,
得三者一起运动的速度大小为u=
v0=
×3=1m/s.
(2)小车向前运动时,轻绳将逐渐伸直.因为轻绳从伸直到拉紧的时间极短,在这极短时间内绳中产生的张力远大于物体对拖车的摩擦力,可以认为仅是小车与拖车间发生了相互作用.对小车与拖车由水平方向动量守恒:
m1v0=(m1+m2)v12,
得绳刚拉紧时两者的共同速度v12=
v0=
×3=
m/s
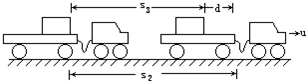
此后,由于物体和拖车间形成了相对速度,拖车对物体产生摩擦力f(f=μm3g),使物体向前(与v12同向)作加速运动,物体对拖车的摩擦力f′(f′=f)使拖车(包括小车)作减速运动,直至物体和拖车(包括小车)以共同速度u运动.在这个过程中,设拖车(包括小车)对地面的位移为s2,物体对地面的位移为s3,对拖车位移为d,如图所示.根据动能定理,对拖车和小车:
-f′s2=
(m1+m2)u2-
(m1+m2)v122
即μm3gs2=
(m1+m2)(v122-u2)
对物体fs3=
m3u2
即μm3gs3=
m3u2
由此解得拖车和物体的位移分别为
s2=
=
m=
m.
s3=
=
m=
m.
所以,物体在拖车平板上移动的距离d=s2-s3=
-
m=
m≈0.33m.
答:(1)当m1、m2、m3以同一速度前进时,速度的大小为1m/s.
(2)物体在拖车平板上移动的距离为0.33m.
得三者一起运动的速度大小为u=
| m1 |
| m1+m2+m3 |
| 20 |
| 20+25+15 |
(2)小车向前运动时,轻绳将逐渐伸直.因为轻绳从伸直到拉紧的时间极短,在这极短时间内绳中产生的张力远大于物体对拖车的摩擦力,可以认为仅是小车与拖车间发生了相互作用.对小车与拖车由水平方向动量守恒:
m1v0=(m1+m2)v12,
得绳刚拉紧时两者的共同速度v12=
| m1 |
| m1+m2 |
| 20 |
| 20+25 |
| 4 |
| 3 |

此后,由于物体和拖车间形成了相对速度,拖车对物体产生摩擦力f(f=μm3g),使物体向前(与v12同向)作加速运动,物体对拖车的摩擦力f′(f′=f)使拖车(包括小车)作减速运动,直至物体和拖车(包括小车)以共同速度u运动.在这个过程中,设拖车(包括小车)对地面的位移为s2,物体对地面的位移为s3,对拖车位移为d,如图所示.根据动能定理,对拖车和小车:
-f′s2=
| 1 |
| 2 |
| 1 |
| 2 |
即μm3gs2=
| 1 |
| 2 |
对物体fs3=
| 1 |
| 2 |
即μm3gs3=
| 1 |
| 2 |
由此解得拖车和物体的位移分别为
s2=
| (m1+m2)(v122-u2) |
| 2μm3g |
(20+25)(
| ||
| 2×0.20×15×10 |
| 7 |
| 12 |
s3=
| u2 |
| 2μg |
| 1 |
| 2×0.20×10 |
| 1 |
| 4 |
所以,物体在拖车平板上移动的距离d=s2-s3=
| 7 |
| 12 |
| 1 |
| 4 |
| 1 |
| 3 |
答:(1)当m1、m2、m3以同一速度前进时,速度的大小为1m/s.
(2)物体在拖车平板上移动的距离为0.33m.
点评:本题综合运用了动量守恒定律、动能定理等知识点,综合性强,关键要合理地选择研究的系统,研究的过程,运用合适的定律进行求解.

练习册系列答案
相关题目
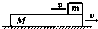 如图所示,在光滑水平面上,有一质量为M=3kg的薄板和质量为m=1kg的物块,都以v=4m/s的初速度朝相反方向运动,它们之间有摩擦,薄板足够长,当薄板的速度为2.4m/s时,物块的运动情况是( )
如图所示,在光滑水平面上,有一质量为M=3kg的薄板和质量为m=1kg的物块,都以v=4m/s的初速度朝相反方向运动,它们之间有摩擦,薄板足够长,当薄板的速度为2.4m/s时,物块的运动情况是( )| A、做加速运动 | B、做减速运动 | C、做匀速运动 | D、以上运动都可能 |
 如图所示,质量为M,半径为R的光滑半圆弧槽静止在光滑水平面上,有一质量为m的小滑块在与圆心等高处无初速度滑下,在小滑块滑到圆弧槽最低点的过程中,圆弧槽产生的位移的大小为( )
如图所示,质量为M,半径为R的光滑半圆弧槽静止在光滑水平面上,有一质量为m的小滑块在与圆心等高处无初速度滑下,在小滑块滑到圆弧槽最低点的过程中,圆弧槽产生的位移的大小为( ) 如图所示,在光滑水平面上,有一辆质量为M的小车,小车的水平上表面放有一质量为m木块,木块与小车间的动摩擦因数为μ,当用一个大小为F的水平恒力拉小车时,小车带着木块保持相对静止而一起向左加速运动.则在运动过程中( )
如图所示,在光滑水平面上,有一辆质量为M的小车,小车的水平上表面放有一质量为m木块,木块与小车间的动摩擦因数为μ,当用一个大小为F的水平恒力拉小车时,小车带着木块保持相对静止而一起向左加速运动.则在运动过程中( ) 如图所示,一个带有1/4圆弧的粗糙滑板A,总质量为mA=3kg,其圆弧部分与水平部分相切于P,水平部分PQ长为L=3.75m.开始时A静止在光滑水平面上,有一质量为mB=2kg的小木块B从滑板A的右端以水平初速度v0=5m/s滑上A,小木块B与滑板A之间的动摩擦因数为μ=0.15,小木块B滑到滑板A的左端并沿着圆弧部分上滑一段弧长后返回最终停止在滑板A上.
如图所示,一个带有1/4圆弧的粗糙滑板A,总质量为mA=3kg,其圆弧部分与水平部分相切于P,水平部分PQ长为L=3.75m.开始时A静止在光滑水平面上,有一质量为mB=2kg的小木块B从滑板A的右端以水平初速度v0=5m/s滑上A,小木块B与滑板A之间的动摩擦因数为μ=0.15,小木块B滑到滑板A的左端并沿着圆弧部分上滑一段弧长后返回最终停止在滑板A上. 在光滑水平面上放有一根平直的弹性轻质长绳,绳上从左向右均匀分布有一系列质点1,2,3,…,相邻两个质点间的距离均为0.10m.在t=0时刻质点1开始沿垂直于绳的方向在水平面内做简谐运动,运动图象如图所示.此振动沿绳向右传播,当振动刚好传播到质点13时,质点1恰好完成第一次全振动.则( )
在光滑水平面上放有一根平直的弹性轻质长绳,绳上从左向右均匀分布有一系列质点1,2,3,…,相邻两个质点间的距离均为0.10m.在t=0时刻质点1开始沿垂直于绳的方向在水平面内做简谐运动,运动图象如图所示.此振动沿绳向右传播,当振动刚好传播到质点13时,质点1恰好完成第一次全振动.则( )