题目内容
水平地面上有一质量为10kg的物体，在几个水平共点力的作用下，向正北方向作匀加速直线运动，加速度的大小为 2m/s2，现突然撤去沿正西方向、大小为15N的一个力，则物体的加速度大小为
2.5
2.5
m/s2，方向为正东偏北53°
正东偏北53°
．分析：突然撤去沿正西方向、大小为15N的一个力；我们可以设想再加上一对沿东西方向的平衡力，故就相当于直接加上一个向正东方向的15N的力，然后根据牛顿第二定律列式求解该力的加速度，最后合成得到合加速度．
解答：解：突然撤去沿正西方向、大小为15N的一个力；
我们可以设想再加上一对沿东西方向的平衡力，故就相当于直接加上一个向正东方向的15N的力；
根据牛顿第二定律，有：F=15=ma′，故a′=
=
=1.5m/s2，正东方向；
故合加速度为：a合=
=2.5m/s2，tanθ=
=
，故θ=53°，正东偏北53°；
故答案为：2.5，正东偏北53°．
我们可以设想再加上一对沿东西方向的平衡力，故就相当于直接加上一个向正东方向的15N的力；
根据牛顿第二定律，有：F=15=ma′，故a′=
| 15 |
| m |
| 15 |
| 10 |
故合加速度为：a合=
| a2+a′2 |
| 2 |
| 1.5 |
| 4 |
| 3 |
故答案为：2.5，正东偏北53°．
点评：本题关键将运动沿着东西和南北正交分解，分别求解出两个方向的合力和加速度，然后合成得到合加速度的大小和方向．
练习册系列答案
相关题目
如图所示，在水平地面上有一质量为4.0kg的物体，它与地面间的动摩擦因数μ=0.2，在与水平方向夹角为37°的斜向上的拉力F作用下，由静止开始运动．经过2.0s物体沿水平面运动了4.0m，g取10m/s2，已知sin37°=0.6，cos37°=0.8．求：
（2010?崇明县一模）在水平地面上有一质量为2kg的物体，物体在水平拉力F的作用下由静止开始运动，10s后拉力大小减为
如图，在水平地面上有一质量为4.0㎏的物块，它与地面的动摩擦因数μ=0.2，在与水平方向夹角为θ=300的斜向上的拉力F作用下，由静止开始运动．经过2.0s的时间物块发生了4.0m的位移．（g=10m/s2）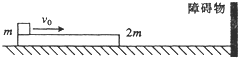 
如图所示，在光滑水平地面上有一质量为2m的长木板，其左端放有一质量为m的重物（可视为质点），重物与长木板之间的动摩擦因数为μ．开始时，长木板和重物都静止，现在给重物以初速度v0，设长木板撞到前方固定的障碍物前，长木板和重物的速度已经相等．已知长木板与障碍物发生弹性碰撞，为使重物始终不从长木板上掉下来，求长木板的长度L至少为多少？（重力加速度度为g）
在水平地面上有一质量为10kg的物体，在水平拉力F的作用下由静止开始运动，10s后拉力大小减为