Question

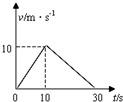在水平地面上有一质量为10kg的物体，在水平拉力F的作用下由静止开始运动，10s后拉力大小减为

F

4

，方向不变，再经过20s停止运动．该物体的速度与时间的关系如图所示．求：
（1）整个过程中物体的位移大小；
（2）物体与地面的动摩擦因数．

Answer 1

分析：（1）整个过程中物体的位移大小等于三角形面积的大小，由数学知识求解．
（2）根据速度图象的斜率等于加速度，求出两段时间内物体的加速度，根据牛顿第二定律和摩擦力公式求解动摩擦因数．

解答：解：（1）整个过程中物体的位移大小等于三角形面积的大小，则得：位移为 x=

1

2

×10×30m=150m．
（2）设加速阶段的加速度大小为a₁，减速阶段的加速度大小为a₂，由v-t图的斜率可知，
 a₁=

△v1

△t1

=

10

10

=1m/s²
 a₂=

△v2

△t2

=

10

20

=0.5m/s²
对物块进行受力分析，由牛顿第二定律可知：
   F-μmg=ma₁
  μmg-

F

4

=ma₂
解得：μ=0.1
答：（1）整个过程中物体的位移大小是150m；
（2）该物体与地面间的动摩擦因数为0.1．

点评：本题首先充分挖掘图象的信息，由斜率等于加速度求得加速度，就可以根据牛顿定律分过程研究F、μ与加速度的关系．