题目内容
 劲度系数为k的轻弹簧,竖直放置在地面上,其上端固定有质量为M的钢板,处于静止状态,如图,现有一质量为m的小球从距钢板H的高处自由下落并与之发生碰撞,碰撞中无机械能损失.已知M=3m,弹簧振子的周期T=2π
劲度系数为k的轻弹簧,竖直放置在地面上,其上端固定有质量为M的钢板,处于静止状态,如图,现有一质量为m的小球从距钢板H的高处自由下落并与之发生碰撞,碰撞中无机械能损失.已知M=3m,弹簧振子的周期T=2π
|
(1)小球与钢板第一次碰撞后,小球的速度v1及钢板的速度v2的大小和方向;
(2)要使小球与钢板每次都在同一高度相碰(即钢板的初始位置),求钢板质量的最大值.
分析:(1)小球碰前做自由落体运动,碰撞过程系统动量和机械能均守恒,根据守恒定律列式后联立求解即可;
(2)要使小球与钢板每次都在同一高度相碰,则小球返回时间为钢板简谐运动半周期的奇数倍,根据等时性列式后联立求解;
(2)要使小球与钢板每次都在同一高度相碰,则小球返回时间为钢板简谐运动半周期的奇数倍,根据等时性列式后联立求解;
解答:解:(1)设小球落至钢板时速度为v0,由机械能守恒定律得,
mgH=
mv02 ①
碰撞过程中动量守恒,mv0=mv1+Mv2 ②
由于机械能无损失,
mv12+
Mv22=
mv02 ③
联立①②③式得,v1=-
v0=-
,负号表示方向向上,
v2=
v0=
,方向竖直向下.
(2)由(1)可知,碰撞后小球做竖直上抛运动,钢板以
v0(连同弹簧)向下做简谐运动,
要使m与M第二次碰撞仍发生在原位置,则必有小球重新落回到O处所用的时间t恰好对应钢板的nT+
T.
而当M取最大值时,必有t=
T,即t=
=
=π
解得,M=
.
答:(1)小球与钢板第一次碰撞后,小球的速度大小是
,方向向上,钢板的速度大小是
,方向竖直向下;
(2)要使小球与钢板每次都在同一高度相碰(即钢板的初始位置),钢板质量的最大值M=
.
mgH=
| 1 |
| 2 |
碰撞过程中动量守恒,mv0=mv1+Mv2 ②
由于机械能无损失,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
联立①②③式得,v1=-
| 1 |
| 2 |
| 1 |
| 2 |
| 2gH |
v2=
| 1 |
| 2 |
| 1 |
| 2 |
| 2gH |
(2)由(1)可知,碰撞后小球做竖直上抛运动,钢板以
| 1 |
| 2 |
要使m与M第二次碰撞仍发生在原位置,则必有小球重新落回到O处所用的时间t恰好对应钢板的nT+
| 1 |
| 2 |
而当M取最大值时,必有t=
| 1 |
| 2 |
| v0 |
| g |
|
|
解得,M=
| 2Hk |
| gπ2 |
答:(1)小球与钢板第一次碰撞后,小球的速度大小是
| 1 |
| 2 |
| 2gH |
| 1 |
| 2 |
| 2gH |
(2)要使小球与钢板每次都在同一高度相碰(即钢板的初始位置),钢板质量的最大值M=
| 2Hk |
| gπ2 |
点评:本题关键明确小球和钢板的运动规律,根据动量守恒定律和机械能守恒定律多次列式后联立求解,第二问找出临界情况是关键,

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上.整个装置处在场强大小为E、方向水平向右的匀强电场中.现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞.碰撞中无机械能损失,且A球的电荷量始终不变.已知B球质量为A球质量的3倍,A、B小球均可视为质点.求:
如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上.整个装置处在场强大小为E、方向水平向右的匀强电场中.现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞.碰撞中无机械能损失,且A球的电荷量始终不变.已知B球质量为A球质量的3倍,A、B小球均可视为质点.求: 如图所示,在一粗糙水平面上有两个质量分别为m和M的木块1和2,M>m,中间用一原长为L、劲度系数为k的轻弹簧连接起来,木块与地面间的动摩擦因数均为μ,若用一水平力F1向左拉木块1,使两木块一起匀速运动时两木块之间的距离是△x1;若用一水平力F2向右拉木块2,使两木块一起匀速运动时两木块之间的距离是△x2,则下列说法正确的是( )
如图所示,在一粗糙水平面上有两个质量分别为m和M的木块1和2,M>m,中间用一原长为L、劲度系数为k的轻弹簧连接起来,木块与地面间的动摩擦因数均为μ,若用一水平力F1向左拉木块1,使两木块一起匀速运动时两木块之间的距离是△x1;若用一水平力F2向右拉木块2,使两木块一起匀速运动时两木块之间的距离是△x2,则下列说法正确的是( ) 如图所示,质量均为m的物体A、B通过一根劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态.现用手通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面,此过程手做功W1、手做功的平均功率为P1;若将A加速向上拉起,A上升的距离为L2时,B刚要离开地面,此过程手做功W2、手做功的平均功率为P2.假设弹簧一直在弹性限度范围内,则( )
如图所示,质量均为m的物体A、B通过一根劲度系数为k的轻弹簧相连,开始时B放在地面上,A、B都处于静止状态.现用手通过细绳缓慢地将A向上提升距离L1时,B刚要离开地面,此过程手做功W1、手做功的平均功率为P1;若将A加速向上拉起,A上升的距离为L2时,B刚要离开地面,此过程手做功W2、手做功的平均功率为P2.假设弹簧一直在弹性限度范围内,则( ) 如图,光滑水平面上带电量为q、质量为m的小球P靠在一劲度系数为k的轻弹簧的右端.现将弹簧向左压缩长度为L后自A点静止释放小球P,小球P运动到B处时恰与静止的不带电的相同小球Q相碰并粘在一起,进入水平向右的匀强电场中.C点右侧是垂直纸面向里的匀强磁场,小球运动到C点时,电场突然变为竖直向上,但大小不变.此后物体开始在竖直平面内作圆周运动,到达最高点时撤去电场,小球正好又落回B点.已知AB=BC=L,弹簧的弹性势能与其形变量x的关系是Ep=
如图,光滑水平面上带电量为q、质量为m的小球P靠在一劲度系数为k的轻弹簧的右端.现将弹簧向左压缩长度为L后自A点静止释放小球P,小球P运动到B处时恰与静止的不带电的相同小球Q相碰并粘在一起,进入水平向右的匀强电场中.C点右侧是垂直纸面向里的匀强磁场,小球运动到C点时,电场突然变为竖直向上,但大小不变.此后物体开始在竖直平面内作圆周运动,到达最高点时撤去电场,小球正好又落回B点.已知AB=BC=L,弹簧的弹性势能与其形变量x的关系是Ep=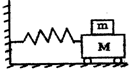 如图中,小车质量为M,木块质量为m它们之间的最大静摩擦力为f,在劲度系数为k的轻弹簧作用下,沿光滑水平面做简谐振动.木块与小车间不发生相对滑动.小车振幅的最大值为多少?
如图中,小车质量为M,木块质量为m它们之间的最大静摩擦力为f,在劲度系数为k的轻弹簧作用下,沿光滑水平面做简谐振动.木块与小车间不发生相对滑动.小车振幅的最大值为多少?