��Ŀ����
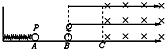
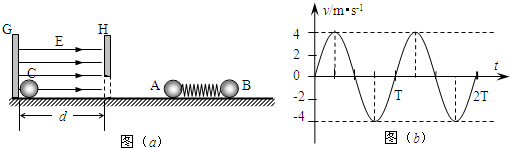
 ��ͼ���⻬ˮƽ���ϴ�����Ϊq������Ϊm��С��P����һ����ϵ��Ϊk���ᵯ�ɵ��Ҷˣ��ֽ���������ѹ������ΪL����A�㾲ֹ�ͷ�С��P��С��P�˶���B��ʱǡ�뾲ֹ�IJ��������ͬС��Q������ճ��һ�𣬽���ˮƽ���ҵ���ǿ�糡�У�C���Ҳ��Ǵ�ֱֽ���������ǿ�ų���С���˶���C��ʱ���糡ͻȻ��Ϊ��ֱ���ϣ�����С���䣮�˺����忪ʼ����ֱƽ������Բ���˶���������ߵ�ʱ��ȥ�糡��С�����������B�㣮��֪AB=BC=L�����ɵĵ������������α���x�Ĺ�ϵ��Ep=
��ͼ���⻬ˮƽ���ϴ�����Ϊq������Ϊm��С��P����һ����ϵ��Ϊk���ᵯ�ɵ��Ҷˣ��ֽ���������ѹ������ΪL����A�㾲ֹ�ͷ�С��P��С��P�˶���B��ʱǡ�뾲ֹ�IJ��������ͬС��Q������ճ��һ�𣬽���ˮƽ���ҵ���ǿ�糡�У�C���Ҳ��Ǵ�ֱֽ���������ǿ�ų���С���˶���C��ʱ���糡ͻȻ��Ϊ��ֱ���ϣ�����С���䣮�˺����忪ʼ����ֱƽ������Բ���˶���������ߵ�ʱ��ȥ�糡��С�����������B�㣮��֪AB=BC=L�����ɵĵ������������α���x�Ĺ�ϵ��Ep=| 1 |
| 2 |
��1���ж�С��P�ĵ��Ժ���B������Ĺ�ͬ�ٶȣ�
��2���糡ǿ��E�ʹŸ�Ӧǿ��B�Ĵ�С��
��3������С��P��A��B�Ĺ�����Ϊ��г�˶���������T=2��
|
��������1��С�����ų�������ֱƽ������Բ���˶���֪С���������͵糡��ƽ�⣬�Ӷ�ȷ����С��ĵ��ԣ����������غ㣬���С����뿪����ʱ���ٶȣ��ٸ��ݶ����غ㶨�������B����Ĺ�ͬ�ٶȣ�
��2�����ݽ���ų���������糡��ƽ�⣬����糡ǿ�ȵĴ�С����ײ��Ľ������Բ���˶�����ߵ㣬��ȥ�糡������ƽ���˶�������ˮƽλ�ƺ��ٶȣ�����˶���ʱ�䣬�Ӷ������ֱ��λ�ƣ�ֱ���������ݴ��������ڴų����˶��İ뾶��ʽ������Ÿ�Ӧǿ�ȵĴ�С��
��3��С���A����������ص�B��Ĺ����пɷ�Ϊ�ĸ����̣���һ��A��B����г�˶����ڶ���B��C���ȼ���ֱ���˶���������Բ���˶�����Ȧ�������Ķ�ƽ���˶����ֱ�����Ķ�ʱ�䣬����ͣ�
��2�����ݽ���ų���������糡��ƽ�⣬����糡ǿ�ȵĴ�С����ײ��Ľ������Բ���˶�����ߵ㣬��ȥ�糡������ƽ���˶�������ˮƽλ�ƺ��ٶȣ�����˶���ʱ�䣬�Ӷ������ֱ��λ�ƣ�ֱ���������ݴ��������ڴų����˶��İ뾶��ʽ������Ÿ�Ӧǿ�ȵĴ�С��
��3��С���A����������ص�B��Ĺ����пɷ�Ϊ�ĸ����̣���һ��A��B����г�˶����ڶ���B��C���ȼ���ֱ���˶���������Բ���˶�����Ȧ�������Ķ�ƽ���˶����ֱ�����Ķ�ʱ�䣬����ͣ�
����⣺��1��С�����ų�����Բ���˶���֪�����͵糡��ƽ�⣮��糡���ķ�����ֱ���ϣ���С��ĵ���Ϊ���磮�� �����غ�ã�
kL2=
mv2
��� v=
�ɶ����غ�ã���ײ��Ĺ�ͬ�ٶ�Ϊv�䣮
mv=2mv��v��=
��2��2mg=qE ��E=
B��C�εļ��ٶ�a=
=g
v12-v��2=2aL
��ȥ�糡����ƽ���˶���ƽ���˶���ʱ��t=
2R=
gt2
���������ڴų����˶�ʱqvB=m
B=
=
(2gL+
)
��3����һ�μ�г�˶���ʱ��t1=
=
�ڶ����ȼ���ֱ���˶���ʱ��t2=
=
�������ڴų����˶���ʱ��t3=
T��=
����t3=
=
���Ķ���ƽ���˶���ʱ��t4=
=
С���A����������ص�B�����ʱ��
t=t1+t2+t3+t4=
+
+
+
| 1 |
| 2 |
| 1 |
| 2 |
��� v=
|
�ɶ����غ�ã���ײ��Ĺ�ͬ�ٶ�Ϊv�䣮
mv=2mv��v��=
|
��2��2mg=qE ��E=
| 2mg |
| q |
B��C�εļ��ٶ�a=
| qE |
| 2m |
v12-v��2=2aL
��ȥ�糡����ƽ���˶���ƽ���˶���ʱ��t=
| L |
| v1 |
2R=
| 1 |
| 2 |
���������ڴų����˶�ʱqvB=m
| v2 |
| R |
B=
| mv1 |
| qR |
| 4m |
| gqL2 |
| kL2 |
| 4m |
| 3 |
| 2 |
��3����һ�μ�г�˶���ʱ��t1=
| T |
| 4 |
| �� |
| 2 |
|
�ڶ����ȼ���ֱ���˶���ʱ��t2=
| v1-v�� |
| a |
| ||||||||
| g |
�������ڴų����˶���ʱ��t3=
| T�� |
| 2 |
T��=
| 2��m |
| qB |
����t3=
| ��m |
| qB |
| ��m | ||||||
|
���Ķ���ƽ���˶���ʱ��t4=
| L |
| v1 |
| L | ||||
|
С���A����������ص�B�����ʱ��
t=t1+t2+t3+t4=
| �� |
| 2 |
|
| ||||||||
| g |
| ��m | ||||||
|
| L | ||||
|
�������������Ĺؼ�������������̵��˶������������м�г�˶����ȼ���ֱ���˶���Բ���˶���ƽ���˶���

��ϰ��ϵ�д�
 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
�����Ŀ

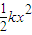 ��ʽ��kΪ���ɵľ���ϵ������
��ʽ��kΪ���ɵľ���ϵ������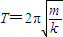 ����С���A����������ص�B�����ʱ�䣮
����С���A����������ص�B�����ʱ�䣮