题目内容
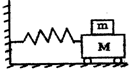如图中，小车质量为M，木块质量为m它们之间的最大静摩擦力为f，在劲度系数为k的轻弹簧作用下，沿光滑水平面做简谐振动．木块与小车间不发生相对滑动．小车振幅的最大值为多少？分析：当物体达到最大位移处时，加速度最大，静摩擦力最大．先对M和m整体，根据牛顿第二定律求出加速度，再对m，由牛顿第二定律列式，即可求出振幅的最大值．
解答：解：当M与m间的静摩擦力达到最大值f时，二者做简谐运动的振幅最大，设为A，此时二者的加速度相同，设为a．
先对M和m组成的整体研究，由牛顿第二定律有：kA=（m+M）a
再隔离m，对m由牛顿第二定律有：f=ma
解得：A=
答：小车振幅的最大值为
．
先对M和m组成的整体研究，由牛顿第二定律有：kA=（m+M）a
再隔离m，对m由牛顿第二定律有：f=ma
解得：A=
| (m+M)f |
| km |
答：小车振幅的最大值为
| (m+M)f |
| km |
点评：题目中m受到的静摩擦力提供回复力，根据整体法求解加速度，根据牛顿第二定律求解静摩擦力．
练习册系列答案
相关题目
