题目内容
(15分)如图所示,用长为L的细线一端系住质量为m的小球,另一端固定在A点,AB是过A的竖直线,E为AB上的一点,且AE=0.5L,过E作水平线EF,在EF上可以钉铁钉D,现将细线水平拉直,然后小球由静止释放。不计一切摩擦,不计线与钉子碰撞时的能量损失,求: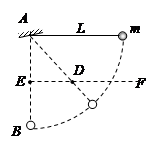
(1)若无铁钉D,小球运动到最低点B时细线的拉力TB=?
(2)若钉上铁钉D且线拉力足够大,使小球恰能绕钉子在竖直面内做完整圆周运动,则钉子D 与点E 距离DE=?
(3)钉铁钉D后,若线能承受的最大拉力是9mg,小球能绕钉子在竖直面内做完整圆周运动,ED取值范围是多少?
(1)3mg;(2)x2≥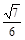 l ;(3)
l ;(3)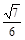 l≤x≤
l≤x≤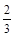 l
l
解析试题分析:(1)这是一个圆周运动与机械能两部分知识综合应用的典型问题.题中涉及两个临界条件:一是线承受的最大拉力不大于9mg;另一个是在圆周运动的最高点的瞬时速度必须不小于 (r是做圆周运动的半径).设在D点绳刚好承受最大拉力,设DE=x1,则:AD=
(r是做圆周运动的半径).设在D点绳刚好承受最大拉力,设DE=x1,则:AD=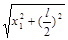
悬线碰到钉子后,绕钉做圆周运动的半径为:r1=l-AD= l-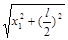 ……①
……①
取B点,EP=0,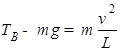 ,mgL=
,mgL=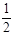 mv2,则TB=3mg。
mv2,则TB=3mg。
(2)设钉子在G点小球刚能绕钉做圆周运动到达圆的最高点,设EG=x2,如图,则:AG=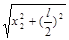
r2=l-AG= l-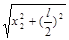 ⑥
⑥
在最高点:mg≤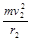 ⑦
⑦
由机械能守恒定律得:mg (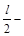 r2)=
r2)=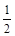 mv22 ⑧
mv22 ⑧
由④⑤⑥联立得:x2≥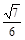 l ⑨
l ⑨
(3)当小球落到D点正下方时,绳受到的最大拉力为F,此时小球的速度v,由牛顿第二定律有:
F-mg=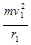 ②
②
结合F≤9mg可得: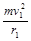 ≤8mg… ③
≤8mg… ③
由机械能守恒定律得:mg (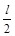 +r1)=
+r1)=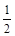 mv12
mv12
即:v2=2g(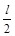 +r1) … ④
+r1) … ④
由①②③式联立解得:x1≤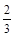 l… ⑤
l… ⑤
随着x的减小,即钉子左移,绕钉子做圆周运动的半径越来越大.转至最高点的临界速度 也越来越大,但根据机械能守恒定律,半径r越大,转至最高点的瞬时速度越小,当这个瞬时速度小于临界速度时,小球就不能到达圆的最高点了.在水平线上EF上钉子的位置范围是:
也越来越大,但根据机械能守恒定律,半径r越大,转至最高点的瞬时速度越小,当这个瞬时速度小于临界速度时,小球就不能到达圆的最高点了.在水平线上EF上钉子的位置范围是: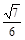 l≤x≤
l≤x≤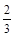 l
l
考点:机械能守恒定律及牛顿定律的应用。

 字词句段篇系列答案
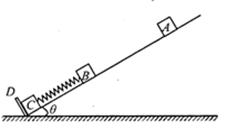
字词句段篇系列答案如右图所示,用皮带输送机将物块m向上传送,两者间保持相对静止,则下列关于m所受摩擦力 的说法正确的是( )
的说法正确的是( )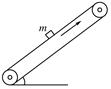
A.皮带传动的速度越大 越大 越大 |
B.皮带加速运动的加速度越大 越小 越小 |
C.皮带速度恒定,m质量越大 越大 越大 |
D. 的方向一定与皮带速度方向相同 的方向一定与皮带速度方向相同 |
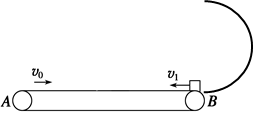
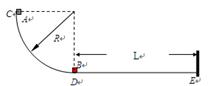
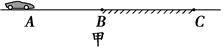


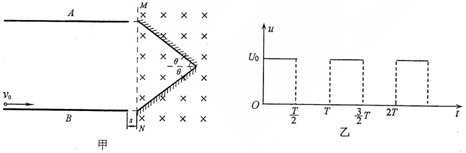
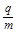 =1.0×108C/kg,初速度v0=2×105m/s(粒子重力不计),在A、B两板间加上如图乙所示的电压,电压的周期T=2.0×10-6s,t=0时刻A板电势高于B板电势,两板间电场可视为匀强电场,电势差U0=360V,A、B板右侧相距s=2cm处有一边界MN,在边界右侧存在一垂直纸面向里的匀强磁场,磁感应强度B=
=1.0×108C/kg,初速度v0=2×105m/s(粒子重力不计),在A、B两板间加上如图乙所示的电压,电压的周期T=2.0×10-6s,t=0时刻A板电势高于B板电势,两板间电场可视为匀强电场,电势差U0=360V,A、B板右侧相距s=2cm处有一边界MN,在边界右侧存在一垂直纸面向里的匀强磁场,磁感应强度B=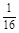 T,磁场中放置一“>”型荧光板,位置如图所示,板与水平方向夹角θ=37°,不考虑粒子之间相互作用及粒子二次进入磁场的可能,求:
T,磁场中放置一“>”型荧光板,位置如图所示,板与水平方向夹角θ=37°,不考虑粒子之间相互作用及粒子二次进入磁场的可能,求: