题目内容
【题目】一质量为m1=1kg、带电量为q=0．5C的小球M以速度v=4．5m/s自光滑平台右端水平飞出，不计空气阻力，小球M飞离平台后由A点沿切线落入竖直光滑圆轨道ABC，圆轨道ABC的形状为半径R＜4m的圆截去了左上角127°的圆弧，CB为其竖直直径，在过A点的竖直线OO’的右边空间存在竖直向下的匀强电场，电场强度大小为E=10V/m，（sin53°=0．8，cos53°=0．6，重力加速度g取10m/s2）
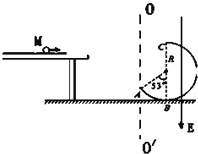
求：
（1）小球M经过A点的速度大小vA；
（2）欲使小球M在圆轨道运动时不脱离圆轨道，求半径R的取值应满足什么条件？
【答案】（1）7．5m/s（2）
或
【解析】试题分析：（1）小球离开平台后做平抛运动，由题知，小球经过A点时的速度沿圆轨道的切线方向，则
解得：
（2）（i）小球N沿切线落入竖直光滑圆轨道ABC后，小球沿轨道做圆周运动，若恰好能通过最高点C，由重力和电场力的合力提供向心力，设滑至最高点的速度为vC，则有
根据动能定理得：
联立以上两式解得
；故当时，小球N沿着轨道做圆周运动的，且能从圆的最高点C飞出．
（ii）若小球N恰好滑到与圆心等高的圆弧上的T点时速度为零，则滑块也沿圆轨道运动而不脱离圆轨道．、根据动能定理得：
解得，
根据题中信息可知
，故当时，小球在轨道内来回的滚动．
综上所述，小球能沿圆轨道运动而不脱离圆轨道，半径R的取值应满足或．
练习册系列答案
相关题目
